题目内容
函数
的单调递减区间是( )
A． | B． | C． | D． |
C
解析试题分析：由题意可知函数的定义域为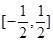
..又有函数
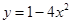在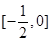
上递增，所以函数
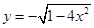在区间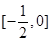上是递减的.故选C.本小题主要是考查复合函数的单调性同增异减.另外要关注定义域的范围.这也是本题的关键.
考点：1.函数的定义域.2.复合函数的单调性.
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
某商场对顾客实行购物优惠活动，规定一次购物付款总额：
(1)如果不超过200元，则不给予优惠；
(2)如果超过200元但不超过500元，则按标价给予9折优惠；
(3)如果超过500元，其500元内的按第(2)条给予优惠，超过500元的部分给予7折优惠.
某人两次去购物，分别付款168元和423元，假设他一次性购买上述两次同样的商品，则应付款是（ ）
| A．413.7元 | B．513.7元 | C．546.6元 | D．548.7元 |
下列函数在区间
上为减函数的是( )
A． | B． | C． | D． |
已知函数
的值域是
，则
的值域是
| A． | B． | C． | D． |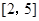
设偶函数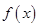
满足
,则不等式
的解集为（ ）
A． 或 | B． 或 |
C．或 | D．或 |
已知函数
，那么
的定义域是
A． | B． |
C． | D． |
是偶函数，则下列各点中必在y=f(x)图象上的是( )
已知函数
是偶函数，且
，当
时，
，则方程
在区间
上的解的个数是（ ）
| A．8 | B．9 | C．10 | D．11 |
若函数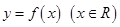
满足
且
时，
，函数
，则函数
在区间
内的零点的个数为 （ ）
| A．7 | B．8 | C．9 | D．10 |