题目内容
已知实数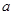 、
、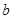 、
、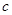 满足
满足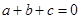 ,
, ,则
,则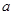 的最大值为为_______.
的最大值为为_______.
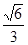
解析试题分析:因为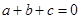 ,所以
,所以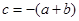 ,
,
所以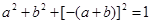 ,
,
所以 ,
,
由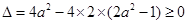 ,解得
,解得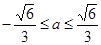 ,
,
故实数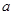 的最大值为
的最大值为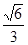 .
.
考点:一元二次方程的根的判别式,容易题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
题目内容
已知实数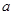 、
、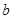 、
、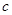 满足
满足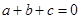 ,
, ,则
,则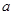 的最大值为为_______.
的最大值为为_______.
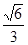
解析试题分析:因为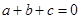 ,所以
,所以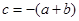 ,
,
所以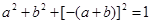 ,
,
所以 ,
,
由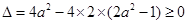 ,解得
,解得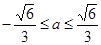 ,
,
故实数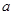 的最大值为
的最大值为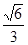 .
.
考点:一元二次方程的根的判别式,容易题.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案