题目内容
用0,1,2,3,4这五个数字组成无重复数字的五位数,其中恰有一个偶数夹在两个奇数之间的五位数共有
28
解析试题分析:0,1,2,3,4中有3个偶数,2个奇数,分3种情况讨论:
①、0被奇数夹在中间,先考虑奇数1、3的顺序,有2种情况;再将1、0、3看成一个整体,与2、4全排列,有A33=6种情况;故0被奇数夹在中间时,有2×6=12种情况;
②、2被奇数夹在中间,先考虑奇数1、3的顺序,有2种情况;再将1、0、3看成一个整体,与2、4全排列,有A33=6种情况,其中0在首位的有2种情况,则有6-2=4种排法;
故2被奇数夹在中间时,有2×4=8种情况;
③、4被奇数夹在中间时,同2被奇数夹在中间的情况,有8种情况,
则这样的五位数共有12+8+8=28种;
故答案为28.
考点:简单排列组合应用问题,计数原理。
点评:中档题,简单排列、组合的应用问题,注意应用分类计数问题。解本题的关键,是要注意数字0不能放在首位,其次列举时要按照顺序进行,做到不重不漏。

练习册系列答案
相关题目
 的展开式中
的展开式中 项的系数为A,则A=___________.
项的系数为A,则A=___________. 轴上的整点),其运动规律为
轴上的整点),其运动规律为 或
或 。若该动点从原点出发,经过6步运动到(6,2)点,则有__________________种不同的运动轨迹。
。若该动点从原点出发,经过6步运动到(6,2)点,则有__________________种不同的运动轨迹。 的展开式中,若第4项是常数项,则n=
的展开式中,若第4项是常数项,则n=  的展开式中,常数项为___________.
的展开式中,常数项为___________. 展开式中的所有二项式系数和为512,则该展开式中
展开式中的所有二项式系数和为512,则该展开式中 的系数为______.
的系数为______. 的展开式中,x的系数是 。(用数字作答)
的展开式中,x的系数是 。(用数字作答) 的展开式的各项系数之和为
的展开式的各项系数之和为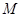 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中
,则展开式中 的系数为___________
的系数为___________ 的展开式中常数项的值是 (数字作答);
的展开式中常数项的值是 (数字作答);