题目内容
设|z |=5,|z
|=5,|z |=2, |z
|=2, |z -
- |=
|= ,求
,求 的值。
的值。
 |=5,|z
|=5,|z |=2, |z
|=2, |z -
- |=
|= ,求
,求 的值。
的值。2±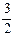 i
i
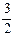 i
i 利用复数模、四则运算的几何意义,将复数问题用几何图形帮助求解。
如图,设z =
=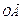 、z
、z =
=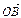 后,则
后,则 =
=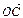 、
、 =
= 如图所示。
如图所示。
由图可知,|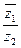 |=
|=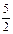 ,∠AOD=∠BOC,由余弦定理得:
,∠AOD=∠BOC,由余弦定理得:
cos∠AOD=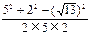 =
=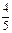 ∴
∴  =
=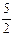 (
(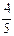 ±
±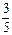 i)=2±
i)=2±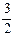 i
i
【另解】设z =
=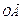 、
、 =
= 如图所示。则|
如图所示。则|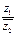 |=
|=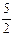 ,且
,且
cos∠AOD=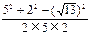 =
=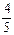 ,sin∠AOD=±
,sin∠AOD=± ,
,
所以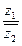 =
=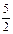 (
( ±
± i)=2±
i)=2±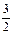 i,即
i,即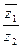 =2±
=2±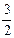 i。
i。
【注】本题运用“数形结合法”,把共轭复数的性质与复平面上的向量表示、代数运算的几何意义等都表达得淋漓尽致,体现了数形结合的生动活泼。 一般地,复数问题可以利用复数的几何意义而将问题变成几何问题,
如图,设z
 =
= 、z
、z =
=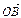 后,则
后,则 =
=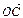 、
、 =
= 如图所示。
如图所示。   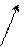    y A y AD O B x C |
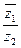 |=
|=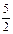 ,∠AOD=∠BOC,由余弦定理得:
,∠AOD=∠BOC,由余弦定理得:cos∠AOD=
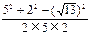 =
=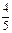 ∴
∴  =
=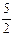 (
(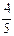 ±
±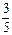 i)=2±
i)=2±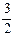 i
i     y A y AD O x |
 =
=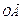 、
、 =
= 如图所示。则|
如图所示。则|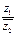 |=
|=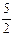 ,且
,且cos∠AOD=
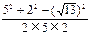 =
=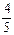 ,sin∠AOD=±
,sin∠AOD=± ,
,所以
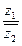 =
=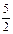 (
( ±
± i)=2±
i)=2±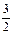 i,即
i,即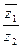 =2±
=2±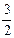 i。
i。【注】本题运用“数形结合法”,把共轭复数的性质与复平面上的向量表示、代数运算的几何意义等都表达得淋漓尽致,体现了数形结合的生动活泼。 一般地,复数问题可以利用复数的几何意义而将问题变成几何问题,

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 (
( 是虚数单位)对应的点位于 ( )
是虚数单位)对应的点位于 ( )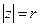 ,求
,求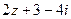 对应的点的轨迹方程.
对应的点的轨迹方程.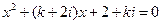 有实根,求这个实根以及实数k的值.
有实根,求这个实根以及实数k的值. ( ).
( ). .
.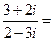




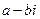 与
与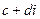 的积是实数的充要条件是 ( )
的积是实数的充要条件是 ( )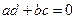



 ,
, ,求满足
,求满足 的复数
的复数 .
.