题目内容
长方体ABCD-A1B1C1D1的各顶点都在球O的球面上,其中AB:AD:AA1=1:1:| 2 |
| m |
| n |
分析:设出AB,求出球的半径,解出A、B两点和A、D1两点的球心角,分别求出球面距离即可;
解答: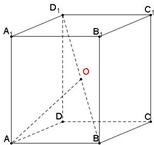 解:设AB=a,则AD=a,AA1=
解:设AB=a,则AD=a,AA1=
a?球的直径2R=
=2a,即R=a
则△OAB是等边三角形,?m=
•2πa=
πa,
在△AOD1中,OA=OD1=a,AD1=
a∠AOD1=120°?n=
•2πa故
=
故答案为:
 解:设AB=a,则AD=a,AA1=
解:设AB=a,则AD=a,AA1=| 2 |
| a2+a2+2a2 |
则△OAB是等边三角形,?m=
| 1 |
| 6 |
| 1 |
| 3 |
在△AOD1中,OA=OD1=a,AD1=
| 3 |
| 1 |
| 3 |
| m |
| n |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查球面距离及其他计算,考查学生空间想象能力,分析问题解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
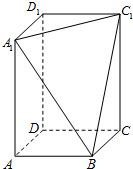 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.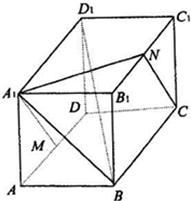 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.