题目内容
已知△ABC, , 则△ABC的面积为( )
, 则△ABC的面积为( )
| A.1 | B.2 | C.3 | D.4 |
A
解析试题分析:因为△ABC, 所以
所以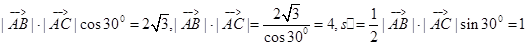 ,故选A。
,故选A。
考点:本题主要考查平面向量的数量积,三角形面积计算。
点评:简单题,计算三角形面积需要知道两边乘积及夹角的正弦,本题利用整体观,从数量积的定义式求得。

练习册系列答案
相关题目
非零向量 ,
,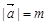 ,
, ,若向量
,若向量 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D.以上均不对 |
设 、
、 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ,
, ,则
,则 的值一定等于( )
的值一定等于( )
A.以 、 、 为两边的三角形面积; 为两边的三角形面积; | B.以 、 、 为邻边的平行四边形的面积; 为邻边的平行四边形的面积; |
C.以 、 、 为两边的三角形面积; 为两边的三角形面积; | D.以 、 、 为邻边的平行四边形的面积. 为邻边的平行四边形的面积. |
 是边长为
是边长为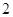 的正三角形,则
的正三角形,则 =( )
=( )
A. | B. | C.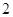 | D. |
已知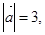
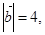
 则
则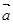 与
与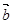 的夹角为 ( )
的夹角为 ( )
A.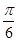 | B.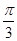 | C.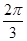 | D. |
在 中,
中,  ,
, 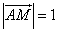 ,点
,点 在
在 上且满足
上且满足 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知平面上不共线的四点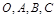 ,若
,若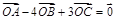 ,则
,则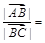
| A.3 | B.4 | C.5 | D.6 |
在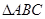 中,
中,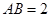 ,
,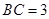 ,
,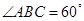 ,
,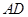 为
为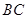 边上的高,
边上的高, 为
为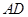 的中点,若
的中点,若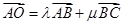 ,则
,则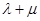 的值为()
的值为()
A.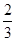 | B.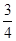 | C.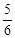 | D.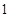 |
设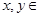 R,向量
R,向量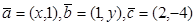 且
且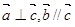 ,则
,则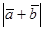 ( )
( )
A.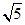 | B. | C.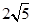 | D.10 |