题目内容
6.已知函数f(x)=xlnx的图象上从左至右依次存在三个点P(p,f(p)),C(c,f(c)),D(d,f(d)),且2c=p+d,求证:f(p)+f(d)-2f(c)<(d-p)ln2.分析 由已知可得0<p<c<d,且c2<pd,进而根据对数的运算性质和基本不等式,利用放缩法,可证得:f(p)+f(d)-2f(c)<(d-p)ln2.
解答 证明:∵函数f(x)=xlnx的图象上从左至右依次存在三个点P(p,f(p)),C(c,f(c)),D(d,f(d)),且2c=p+d,
∴0<p<c<d,且2c=p+d<$2\sqrt{pd}$,即c2<pd,
∴f(p)+f(d)-2f(c)=plnp+dlnd-2clnc
=ln$\frac{{p}^{p}•{d}^{d}}{{c}^{2c}}$=ln$\frac{{(pd)}^{p}•{d}^{d-p}}{{c}^{p+d}}$<ln$\frac{{c}^{2p}•{d}^{d-p}}{{c}^{p+d}}$
=ln(cp-d•dd-p)=ln$(\frac{d}{c})^{d-p}$
=(d-p)ln$\frac{d}{c}$<(d-p)ln$\frac{d+p}{c}$
=(d-p)ln$\frac{2c}{c}$=(d-p)ln2
点评 本题考查的知识点是对数的图象与性质,基本不等式,难度中档.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
15.如图所示,用符号语言可表示为( )
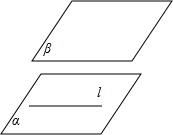

| A. | α∩β=l | B. | α∥β,l∈α | C. | l∥β,l?α | D. | α∥β,l?α |