题目内容
若直角坐标平面内两点P、Q满足条件：①P、Q都在函数y=f（x）的图象上；②P、Q关于原点对称，则点对（P，Q）称为是函数y=f（x）的一个“友好点对”（点对（P，Q）与（Q，P）看作同一个“友好点对”）．已知函数f(x)=
，则f（x）的“友好点对”有（ ）
|
分析：根据“友好点对”的定义可知，只需要利用图象，作出函数f（x）=2x2+4x+1，-2＜x＜0关于原点对称的图象，利用对称图象在0＜x＜2上两个图象的交点个数，即为“友好点对”的个数．
解答：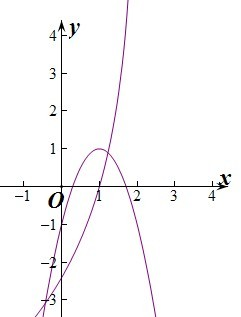
解：由题意知函数f（x）=2x2+4x+1，-2＜x＜0关于原点对称的图象为-y=2x2-4x+1，
即y=-2x2+4x-1，0＜x＜2，
在0＜x＜2上作出两个函数的图象如图，
由图象可知两个函数在0＜x＜2上的交点个数只有一个，所以函数f（x）的“友好点对”有1个，
故选A．
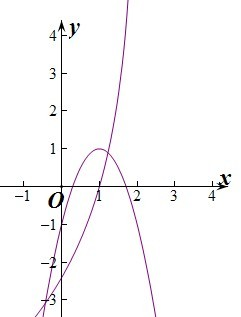解：由题意知函数f（x）=2x2+4x+1，-2＜x＜0关于原点对称的图象为-y=2x2-4x+1，即y=-2x2+4x-1，0＜x＜2，
在0＜x＜2上作出两个函数的图象如图，
由图象可知两个函数在0＜x＜2上的交点个数只有一个，所以函数f（x）的“友好点对”有1个，
故选A．
点评：本题主要考查新定义题目，读懂题意，利用数形结合的思想是解决本题的关键．
练习册系列答案
相关题目
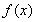
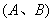
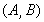
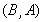
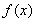
的图象上；②P、Q关于原点对称，则称点对（P，Q）是函数
的一个“友好点对”（点对（P，Q）与（Q，P）看作同一个“友好点对”）．已知函数
则
的“友好点对”有