题目内容
已知圆C:(x-1)2+(y+2)2=9,直线l:(m+1)x-y-2m-3=0(m∈R)(1)求证:无论m取什么实数,直线恒与圆交于两点;
(2)求直线l被圆C所截得的弦长最小时的直线方程.
【答案】分析:(1)将直线l解析式变形得到直线l恒过(2,-1),再判断出此点在圆C内部,即可得到直线与圆相交,即直线恒与圆交于两点,得证;
(2)由垂径定理:(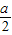 )2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),当d越大的时候,弦长a越小,根据垂线段最短可知,当l⊥CA时,直线l被圆C所截得的弦长最小,根据A与C坐标求出直线AC斜率,进而求出直线l斜率,即可确定出此时直线l的方程.
)2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),当d越大的时候,弦长a越小,根据垂线段最短可知,当l⊥CA时,直线l被圆C所截得的弦长最小,根据A与C坐标求出直线AC斜率,进而求出直线l斜率,即可确定出此时直线l的方程.
解答: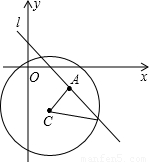 解:(1)∵l:m(x-2)+(x-y-3)=0,
解:(1)∵l:m(x-2)+(x-y-3)=0,
∴直线l恒过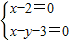 的交点,即(2,-1),
的交点,即(2,-1),
将点(2,-1)代入圆C的方程得(2-1)2+(-1+2)2=2<9,
∴点(2,-1)在圆内,
∴无论m取什么值,直线恒与圆相交;
(2)由垂径定理:(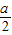 )2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),
)2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),
当d越大的时候,弦长a越小,
根据垂线段最短可知,当l⊥CA时,直线l被圆C所截得的弦长最小,
∵A(2,-1),C(1,-2),
∴kCA=1,
∴kl=-1,
∴直线l的方程为y=-(x-2)-1,即x+y-1=0.
点评:此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r大小来判断,当d>r时,直线与圆相离;当d<r时,直线与圆相交;当d=r时,直线与圆相切(其中d为圆心到直线的距离,r为圆的半径).
(2)由垂径定理:(
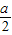 )2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),当d越大的时候,弦长a越小,根据垂线段最短可知,当l⊥CA时,直线l被圆C所截得的弦长最小,根据A与C坐标求出直线AC斜率,进而求出直线l斜率,即可确定出此时直线l的方程.
)2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),当d越大的时候,弦长a越小,根据垂线段最短可知,当l⊥CA时,直线l被圆C所截得的弦长最小,根据A与C坐标求出直线AC斜率,进而求出直线l斜率,即可确定出此时直线l的方程.解答:
 解:(1)∵l:m(x-2)+(x-y-3)=0,
解:(1)∵l:m(x-2)+(x-y-3)=0,∴直线l恒过
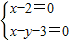 的交点,即(2,-1),
的交点,即(2,-1),将点(2,-1)代入圆C的方程得(2-1)2+(-1+2)2=2<9,
∴点(2,-1)在圆内,
∴无论m取什么值,直线恒与圆相交;
(2)由垂径定理:(
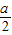 )2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),
)2=r2-d2(a表示弦长,r表示半径,d表示圆心到直线的距离),当d越大的时候,弦长a越小,
根据垂线段最短可知,当l⊥CA时,直线l被圆C所截得的弦长最小,
∵A(2,-1),C(1,-2),
∴kCA=1,
∴kl=-1,
∴直线l的方程为y=-(x-2)-1,即x+y-1=0.
点评:此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r大小来判断,当d>r时,直线与圆相离;当d<r时,直线与圆相交;当d=r时,直线与圆相切(其中d为圆心到直线的距离,r为圆的半径).

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目