题目内容
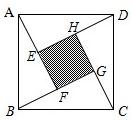 “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).某同学随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到小正方形(阴影)区域的概率是( )
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).某同学随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到小正方形(阴影)区域的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据几何概型的意义,求出小正方形的面积,再求出大正方形的面积,算出其比值即可.
解答:解:根据题意分析可得:
正方形ABCD边长为
=
,故面积为5;
阴影部分边长为2-1=1,面积为1;
则针扎到小正方形(阴影)区域的概率是即两部分面积的比值为
.
故选D.
正方形ABCD边长为
| 22+12 |
| 5 |
阴影部分边长为2-1=1,面积为1;
则针扎到小正方形(阴影)区域的概率是即两部分面积的比值为
| 1 |
| 5 |
故选D.
点评:本题考查几何概型的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积和总面积的比,这个比即事件(A)发生的概率.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
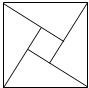 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于 2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为
2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为 2002年8月在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,则sin2θ-cos2θ的值等于( )
2002年8月在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,则sin2θ-cos2θ的值等于( )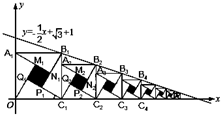 2002年在北京召开的世界数学家大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线
2002年在北京召开的世界数学家大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线