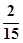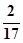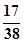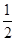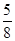题目内容
某类种子每粒发芽的概率是90%,现播种该种子1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望与方差分别是( )
| A.100 90 | B.100 180 | C.200 180 | D.200 360 |
D
解析试题分析:由题意可知播种了1000粒,没有发芽的种子数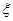 服从二项分布,即
服从二项分布,即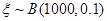 ,而每粒需再补种2粒,补种的种子数记为X,故
,而每粒需再补种2粒,补种的种子数记为X,故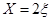 ,则
,则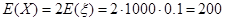 ,
,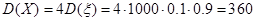 .
.
考点:1.二项分布的期望与方差;2.随机变量的性质.

练习册系列答案
相关题目
已知随机变量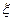 服从正态分布N(2,σ2),且P(
服从正态分布N(2,σ2),且P(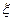 <4)=0.8,则P(0<
<4)=0.8,则P(0<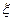 <2)=( )
<2)=( )
| A.0.6 | B.0.4 | C.0.3 | D.0.2 |
给出如下四对事件:
①某人射击1次,“射中7环”与“射中8环”;
②甲、乙两人各射击1次,“甲射中7环”与“乙射中8环”;
③甲、乙两人各射击1次,“两人均射中目标”与“两人均没有射中目标”;
④甲、乙两人各射击1次,“至少有1人射中目标”与“甲射中,但乙未射中目标”,
其中属于互斥事件的有( )
| A.1对 | B.2对 | C.3对 | D.4对 |
一数学兴趣小组利用几何概型的相关知识做试验计算圆周率,他们向一个边长为1米的正方形区域均匀撒豆,测得正方形区域有豆5120颗,正方形的内切圆区域有豆4009颗,则他们所测得的圆周率约为(保留三位有效数字)( )
| A.3.13 | B.3.14 | C.3.15 | D.3.16 |
在5件产品中,有3件一等品和2件二等品,从中任取2件,以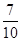 为概率的事件是( )
为概率的事件是( )
| A.都不是一等品 | B.恰有1件一等品 |
| C.至少有1件一等品 | D.至多有1件一等品 |
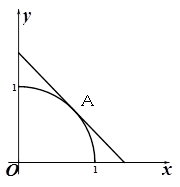
 与两坐标轴正半轴围成的扇形区域为
与两坐标轴正半轴围成的扇形区域为 ,过圆弧上一点
,过圆弧上一点 做该圆的切线与两坐标轴正半轴围成的三角形区域为
做该圆的切线与两坐标轴正半轴围成的三角形区域为 .现随机在区域
.现随机在区域 内投一点
内投一点 ,若设点
,若设点 内的概率为
内的概率为 ,则
,则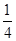
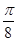
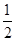
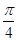
 张假钞的
张假钞的 张百元钞票中任意抽取
张百元钞票中任意抽取 张,将其中一张在验钞机上检验发现是假钞,问这
张,将其中一张在验钞机上检验发现是假钞,问这