题目内容
(本大题共12分)
如图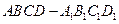 为正
为正 方体,一只青蛙开始在顶点A处,它每次可随意
方体,一只青蛙开始在顶点A处,它每次可随意 跳到相邻三顶点之一,若在五次内跳到
跳到相邻三顶点之一,若在五次内跳到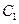 点,则停止跳动;若5次内不能跳到
点,则停止跳动;若5次内不能跳到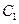 点,跳完五
点,跳完五 次也停止跳动,求:
次也停止跳动,求: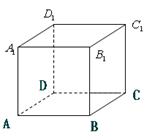
(1)5次以内能到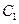 点的跳法有多少种?
点的跳法有多少种?
(2)从开始到停止,可能出现的跳法有多少种?
解:(1)如果不回跳,那么跳三次可到达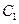 点,第一
点,第一 跳有3
跳有3 种;第二跳有2种;第三跳有1种,共有
种;第二跳有2种;第三跳有1种,共有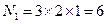 种。
种。 (2)由条件青蛙的跳法只可能出现两种情况,
(2)由条件青蛙的跳法只可能出现两种情况,
其一,跳三次到达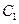 点,有6种跳法,
点,有6种跳法,
其二,跳五次停止(前三次不到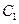 点),有
点),有 ,
,
故共有6+189=195种不同的跳法。
解析

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
(本小题共12分)
某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
,![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
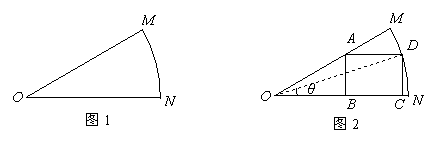 |
(Ⅰ)用含![]() 的式子表示
的式子表示![]() 、
、![]() 的长;
的长;
(Ⅱ)试将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅲ)求![]() 的最大值.
的最大值.
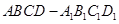 为正方体,一只青蛙开始在顶点A处,它每次可随意跳到相邻三顶点之一,若在五次内跳到
为正方体,一只青蛙开始在顶点A处,它每次可随意跳到相邻三顶点之一,若在五次内跳到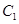 点,则停止跳动;若5次内不能跳到
点,则停止跳动;若5次内不能跳到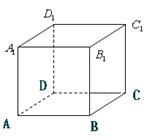
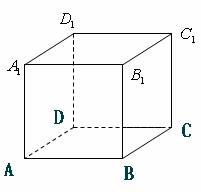 如图
如图