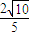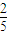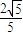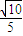题目内容
已知直线和参数方程为
(t为参数),P是椭圆
+y2=1上任意一点,则点P到直线的距离的最大值为( )
|
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先将利用消参法将直线的参数方程化成直线的普通方程,再利用椭圆的参数方程设出点P的坐标,利用点到直线的距离求最大值即可.
解答:解:直线的参数方程为
为参数)故直线的普通方程为x+2y=0
因为为椭圆
+y2=1上任意点,故可设P(2cosθ,sinθ)其中θ∈R.
因此点到直线的距离是d=
=
所以当θ=kπ+
,时,取得最大值,最大值为
.
故选A.
|
因为为椭圆
| x2 |
| 4 |
因此点到直线的距离是d=
| |2cosθ+2sinθ| | ||
|
2
| ||||
|
所以当θ=kπ+
| π |
| 4 |
2
| ||
| 5 |
故选A.
点评:本题主要考查了直线和椭圆的参数方程,以及点到直线的距离公式等基础知识,属于基础题.

练习册系列答案
相关题目
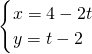 (t为参数),P是椭圆
(t为参数),P是椭圆 上任意一点,则点P到直线的距离的最大值为
上任意一点,则点P到直线的距离的最大值为



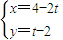 (t为参数),P是椭圆
(t为参数),P是椭圆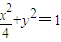 上任意一点,则点P到直线的距离的最大值为( )
上任意一点,则点P到直线的距离的最大值为( )