题目内容
设函数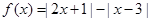 .
.
(1)解不等式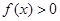 ;
;
(2)已知关于x的不等式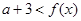 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:
解题思路:(1)化简 的解析式,得到分段函数,再分段求解不等式;(2)将关于x的不等式
的解析式,得到分段函数,再分段求解不等式;(2)将关于x的不等式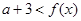 恒成立转化为
恒成立转化为 即可.
即可.
规律总结:1.对于含两个绝对值的函数,往往根据 ,讨论
,讨论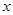 的不同范围,将其绝对值符号脱去,转化为分段函数问题;2.对于不等式恒成立,一般思路将参数分离,转化为求函数的最值问题.
的不同范围,将其绝对值符号脱去,转化为分段函数问题;2.对于不等式恒成立,一般思路将参数分离,转化为求函数的最值问题.
试题解析:(1)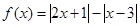 可化为
可化为 ,
,
则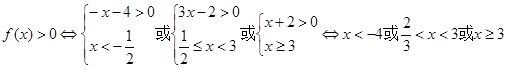 ,
,
即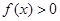 的解集为
的解集为 ;
;
当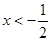 时,
时,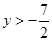 ;当
;当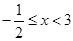 时,
时,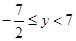 ;当
;当 时,
时, ;即
;即 的最小值为
的最小值为 ;因为关于x的不等式
;因为关于x的不等式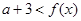 恒成立,所以
恒成立,所以 ,即实数
,即实数 的取值范围
的取值范围 .
.
考点:1.绝对值不等式;2.不等式恒成立.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
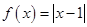 .
.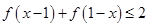 ;
; 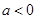 ,求证:
,求证: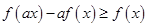
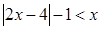 .
.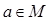 ,求证:
,求证: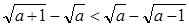
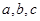 为三角形
为三角形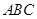 的三边,求证:
的三边,求证: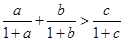
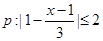 ,
, ,若
,若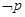 是
是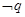 的充分不必要条件,求实数
的充分不必要条件,求实数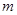 的取值范围.
的取值范围.