题目内容
6.已知椭圆C的中心为坐标原点,焦点在坐标轴上,且经过点M(4,1),N(2,2).(1)求椭圆C的方程;
(2)若斜率为1的直线l与椭圆C交于不同的两点A,B,且|AB|=$\frac{16\sqrt{3}}{5}$,求直线l的方程.
分析 (1)设椭圆的方程为mx2+ny2=1,代入N.M的坐标,解方程即可得到所求;
(2)设出直线l的方程y=x+t,代入椭圆方程,运用判别式大于0和韦达定理,弦长公式,解方程可得t,即可得到所求直线方程.
解答 解:(1)设椭圆的方程为mx2+ny2=1,
代入M(4,1),N(2,2),即有
$\left\{\begin{array}{l}{16m+n=1}\\{4m+4n=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{1}{20}}\\{n=\frac{1}{5}}\end{array}\right.$,
则椭圆的方程为$\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1;
(2)设直线l的方程为y=x+t,
代入椭圆的方程可得,5x2+8tx+4t2-20=0,
判别式为△=64t2-20(4t2-20)>0,
设A(x1,y1),B(x2,y2),
x1+x2=-$\frac{8t}{5}$,x1x2=$\frac{4{t}^{2}-20}{5}$,
即有}AB|=$\sqrt{1+1}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{2}$•$\sqrt{(-\frac{8t}{5})^{2}-\frac{4(4{t}^{2}-20)}{5}}$=$\frac{16\sqrt{3}}{5}$,
解得t=±1,检验判别式大于0成立.
则所求直线l的方程为y=x+1或y=x-1.
点评 本题考查椭圆的方程的求法,注意设出椭圆的方程为mx2+ny2=1,同时考查直线和椭圆相交的弦长问题,考查运算能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.过点P(2,-1)作圆(x-1)2+y2=25的弦AB,则弦长AB的最短时AB所在的直线方程方程是( )
| A. | x-y-3=0 | B. | 2x+y-3=0 | C. | x+y-1=0 | D. | 2x-y-5=0 |
14.为了研究“教学方式”对教学质量的影响,某高中英语老师分别用两种不同的教学方法对入学英语平均分和优秀率都相同的甲乙两个高一新班进行教学(勤奋程度和自觉性相同),以下茎叶图为甲乙两班(每班均20人)学生的英语期末成绩,若成绩不低于125分的为优秀,填写下面的2×2列联表,并判断是否有97.5%的把握认为“成绩优秀与教学方式有关”.
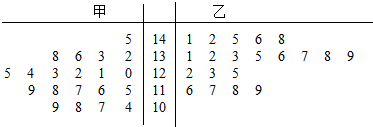
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{{n}_{+2}}^{\;}}$
附表:

| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
附表:
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18.与向量$\overrightarrow{a}$=(2,2)方向相同的单位向量是( )
| A. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | B. | (1,1) | C. | (-1,-1) | D. | ($\frac{1}{2}$,$\frac{1}{2}$) |
16.下列说法不正确的是( )
| A. | 空间中,一组对边平行且相等的四边形是一定是平行四边形 | |
| B. | 同一平面的两条垂线一定共面 | |
| C. | 三角形一定是平面图形 | |
| D. | 过一条直线有且只有一个平面与已知平面垂直 |
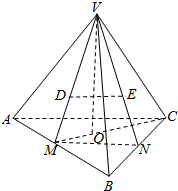 如图所示,已知D,E分别是三棱锥V-ABC的两个侧面VAB,VBC的重心.
如图所示,已知D,E分别是三棱锥V-ABC的两个侧面VAB,VBC的重心.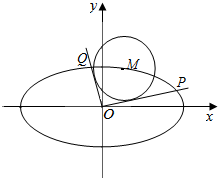 如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.