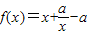题目内容
已知函数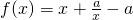
(I) 若f(x)>0对任意x∈(1,+∞)恒成立,求实数a的取值范围;(II)解关于x的不等式f(x)>1.
解:由题意,(I)问题等价于 对任意x∈(1,+∞)恒成立;
对任意x∈(1,+∞)恒成立;
∵x∈(1,+∞),∴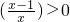 ,∴
,∴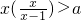
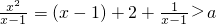
∵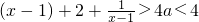
(II)不等式可化为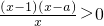
a<0时x∈(a,0)∪(1,+∞);a=0时x∈(1,+∞)0<a<1时x∈(0,a)∪(1,+∞)a=1时x∈(0,1)∪(1,+∞)a>1时x∈(0,1)∪(a,+∞)
分析:(I) 根据x∈(1,+∞),将问题等价于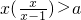 ,从而利用基本不等式求最值,进而可求实数a的取值范围;(II)不等式可化为
,从而利用基本不等式求最值,进而可求实数a的取值范围;(II)不等式可化为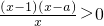 ,对参数a进行分类讨论,从而可确定不等式的解集.
,对参数a进行分类讨论,从而可确定不等式的解集.
点评:本题以函数为载体,考查恒成立问题,考查解不等式,关键是等价转化.
 对任意x∈(1,+∞)恒成立;
对任意x∈(1,+∞)恒成立;∵x∈(1,+∞),∴
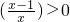 ,∴
,∴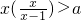
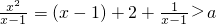
∵
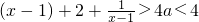
(II)不等式可化为
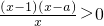
a<0时x∈(a,0)∪(1,+∞);a=0时x∈(1,+∞)0<a<1时x∈(0,a)∪(1,+∞)a=1时x∈(0,1)∪(1,+∞)a>1时x∈(0,1)∪(a,+∞)
分析:(I) 根据x∈(1,+∞),将问题等价于
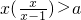 ,从而利用基本不等式求最值,进而可求实数a的取值范围;(II)不等式可化为
,从而利用基本不等式求最值,进而可求实数a的取值范围;(II)不等式可化为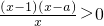 ,对参数a进行分类讨论,从而可确定不等式的解集.
,对参数a进行分类讨论,从而可确定不等式的解集.点评:本题以函数为载体,考查恒成立问题,考查解不等式,关键是等价转化.

练习册系列答案
相关题目

 平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的单调区间及值域.
平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的单调区间及值域.
 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
 成立,求实数a的取值范围;
成立,求实数a的取值范围;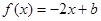 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.