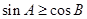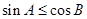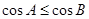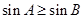题目内容
已知A,B,C为△ABC的三个内角,其所对的边分别为a,b,c,若A=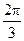 ,a=2
,a=2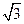 ,b+c=4,则△ABC的面积为( )
,b+c=4,则△ABC的面积为( )
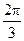 ,a=2
,a=2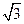 ,b+c=4,则△ABC的面积为( )
,b+c=4,则△ABC的面积为( )A.2 |
B. |
C.3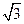 |
D.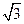 |
D
由余弦定理得,
a2=b2+c2-2bccos A,A=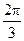 ,则a2=(b+c)2-bc,
,则a2=(b+c)2-bc,
又a=2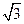 ,b+c=4,有12=42-bc,则bc=4,
,b+c=4,有12=42-bc,则bc=4,
故S△ABC=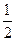 bcsin A=
bcsin A=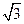 .
.
a2=b2+c2-2bccos A,A=
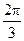 ,则a2=(b+c)2-bc,
,则a2=(b+c)2-bc,又a=2
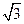 ,b+c=4,有12=42-bc,则bc=4,
,b+c=4,有12=42-bc,则bc=4,故S△ABC=
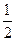 bcsin A=
bcsin A=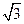 .
.
练习册系列答案
相关题目
 ,则△ABC面积的最大值为( )
,则△ABC面积的最大值为( )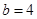 ,
,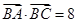 .
.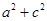 的值;
的值; 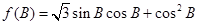 的值域.
的值域. ,b=1,c=2,则A等于____________.
,b=1,c=2,则A等于____________. 中,已知
中,已知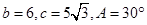 ,则
,则 =
= 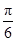 ,c=2
,c=2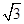 ,则b= .
,则b= . 的内角
的内角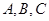 所对的边分别为
所对的边分别为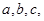 且
且 ,则角
,则角 ;
; ABC中,角A、B、C的对边分别为a、b、c,若
ABC中,角A、B、C的对边分别为a、b、c,若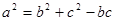 ,则角A等于
,则角A等于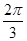 B.
B.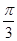 C.
C. D.
D.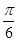
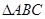 中,
中,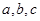 分别是内角
分别是内角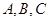 所对的边,且
所对的边,且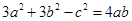 ,则下列结论正确的是
,则下列结论正确的是