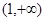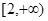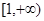题目内容
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+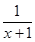 的值域,集合C为不等式
的值域,集合C为不等式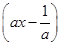 (x+4)≤0的解集.
(x+4)≤0的解集.
(1)求A∩B;
(2)若C⊆∁RA,求a的取值范围.
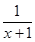 的值域,集合C为不等式
的值域,集合C为不等式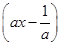 (x+4)≤0的解集.
(x+4)≤0的解集.(1)求A∩B;
(2)若C⊆∁RA,求a的取值范围.
(1)A∩B={x|-4<x≤-3或1≤x<2} (2)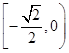
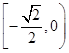
解:(1)由-x2-2x+8>0得-4<x<2,
即A={x|-4<x<2}.
y=x+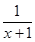 =(x+1)+
=(x+1)+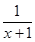 -1,当x+1>0,即x>-1时,y≥2-1=1,此时x=0,符合题意;当x+1<0,即x<-1时,y≤-2-1=-3,此时x=-2,符合题意.所以B={x|x≤-3或x≥1},所以A∩B={x|-4<x≤-3或1≤x<2}.
-1,当x+1>0,即x>-1时,y≥2-1=1,此时x=0,符合题意;当x+1<0,即x<-1时,y≤-2-1=-3,此时x=-2,符合题意.所以B={x|x≤-3或x≥1},所以A∩B={x|-4<x≤-3或1≤x<2}.
(2)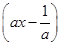 (x+4)=0有两根x=-4或x=
(x+4)=0有两根x=-4或x=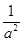 .
.
当a>0时,C=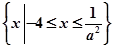 ,不可能有C⊆∁RA;
,不可能有C⊆∁RA;
当a<0时,C=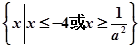 ,
,
若C⊆∁RA,则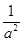 ≥2,∴a2≤
≥2,∴a2≤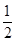 ,
,
∴-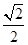 ≤a<0.
≤a<0.
故a的取值范围为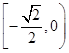 .
.
即A={x|-4<x<2}.
y=x+
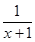 =(x+1)+
=(x+1)+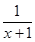 -1,当x+1>0,即x>-1时,y≥2-1=1,此时x=0,符合题意;当x+1<0,即x<-1时,y≤-2-1=-3,此时x=-2,符合题意.所以B={x|x≤-3或x≥1},所以A∩B={x|-4<x≤-3或1≤x<2}.
-1,当x+1>0,即x>-1时,y≥2-1=1,此时x=0,符合题意;当x+1<0,即x<-1时,y≤-2-1=-3,此时x=-2,符合题意.所以B={x|x≤-3或x≥1},所以A∩B={x|-4<x≤-3或1≤x<2}.(2)
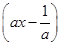 (x+4)=0有两根x=-4或x=
(x+4)=0有两根x=-4或x=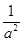 .
.当a>0时,C=
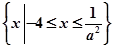 ,不可能有C⊆∁RA;
,不可能有C⊆∁RA;当a<0时,C=
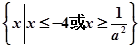 ,
,若C⊆∁RA,则
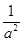 ≥2,∴a2≤
≥2,∴a2≤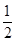 ,
,∴-
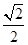 ≤a<0.
≤a<0.故a的取值范围为
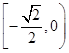 .
.
练习册系列答案
相关题目
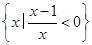 ,B={x|x≥1},则集合{x|x≤0}等于( )
,B={x|x≥1},则集合{x|x≤0}等于( ) ),则图中阴影部分所表示的集合为( )
),则图中阴影部分所表示的集合为( )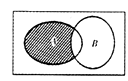
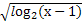 },B={y|y=
},B={y|y=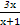 },则A∩B=( )
},则A∩B=( )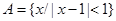 ,
,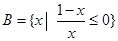 ,则A∩(∁UB)=( )
,则A∩(∁UB)=( )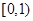 C.(1, 2) D. (0,2)
C.(1, 2) D. (0,2)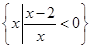 ,T={x|x2-(2a+1)x+a2+a≥0}(a∈R),则S∪T=R的充要条件是________.
,T={x|x2-(2a+1)x+a2+a≥0}(a∈R),则S∪T=R的充要条件是________.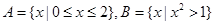 ,则
,则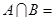 ( )
( )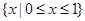
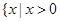 或
或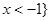
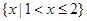
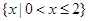
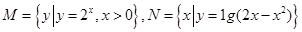 ,则
,则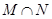 为( )
为( )