题目内容
已知某校5个学生的数学和物理成绩如下表:
(Ⅰ)通过大量事实证明发现,学生的数学成绩和物理成绩具有很强的线性相关关系,用x表示数学成绩,用y表示物理成绩,根据上述表格求y与x的回归方程;
(Ⅱ)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式和数据:回归直线方程:
=bx+a,其中b=
,a=
-b
;
xiyi=23190,
=24750,残差和公式为:
(yi-
i).
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式和数据:回归直线方程:
| ? |
| y |
| |||||||
|
. |
| y |
. |
| x |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| ? |
| y |
分析:(I)分别做出横标和纵标的平均数,利用最小二乘法做出b的值,再做出a的值,写出线性回归方程,得到结果.
(II)做出残差平方差,得到结果是0,根据所给的残差平方和的范围,得到所求的线性回归方程是一个优逆方程.
(II)做出残差平方差,得到结果是0,根据所给的残差平方和的范围,得到所求的线性回归方程是一个优逆方程.
解答:解:(I)
=70,
=66,
b=
=0.36,
a=40.8,
∴回归直线方程为y=0.36x+40.8.
(Ⅱ)∵残差和公式为:
(yi-
)=0,
∵0∈(-0.1,0.1),
∴回归方程为优逆方程.
. |
| x |
. |
| y |
b=
| 80×70+75×66+70×68+65×64+60×62-5×70×66 |
| 802+752+702+652+602-5×702 |
a=40.8,
∴回归直线方程为y=0.36x+40.8.
(Ⅱ)∵残差和公式为:
| 5 |
 |
| i=1 |
 |
| yi |
∵0∈(-0.1,0.1),
∴回归方程为优逆方程.
点评:本题考查变量间的相关关系,考查回归分析的应用,考查新定义问题,是一个基础题,注意题目的数字运算不要出错.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7. 11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.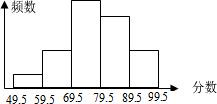 武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行评比,下面是将某年级60篇学生调查报告的成绩进行整理,分成五组画出的频数分布直方图.已知从左至右5个小组的频数之比为1:3:7:6:3,则在这次评比中被评为优秀的调查报告(分数大于或等于80分为优秀,且分数为整数)占百分之( )
武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行评比,下面是将某年级60篇学生调查报告的成绩进行整理,分成五组画出的频数分布直方图.已知从左至右5个小组的频数之比为1:3:7:6:3,则在这次评比中被评为优秀的调查报告(分数大于或等于80分为优秀,且分数为整数)占百分之( ) 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的 一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的 一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7. 为了解某校学生数学竞赛的成绩分布,从该校参加数学竞赛的学生成绩中抽取一个样本,并分成5组,绘成频率分布直方图如图,从左到右各小组的小长方形的高之比为1:2:2:20:5,最右边一组的频数是20,请结合直方图的信息,解答下列问题;
为了解某校学生数学竞赛的成绩分布,从该校参加数学竞赛的学生成绩中抽取一个样本,并分成5组,绘成频率分布直方图如图,从左到右各小组的小长方形的高之比为1:2:2:20:5,最右边一组的频数是20,请结合直方图的信息,解答下列问题;