题目内容
已知数列(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() .若对任意正整数
.若对任意正整数![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
解答:本题主要考查数列的通项公式的求解以及数列的求和和不等式的综合问题,考查逻辑思维能力.
(1)![]()
![]() , ①
, ①
∴当![]() 时,
时,![]() . ②
. ②
由①-②,得![]() .
.
∴![]()
![]()
又 ![]() ,
,![]() ,解得
,解得 ![]() .
.
∴数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
∴![]() (
(![]() 为正整数)
为正整数)
(2)由(1)知,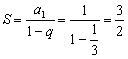 ,
,
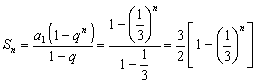
由题意可知,对于任意的正整数![]() ,恒有
,恒有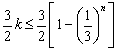 ,解得
,解得![]() .
.
![]() 数列
数列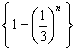 单调递增,∴当
单调递增,∴当![]() 时,数列中的最小项为
时,数列中的最小项为![]() ,
,
∴必有![]() ,即实数
,即实数![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式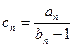 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.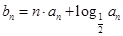 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.