题目内容
已知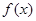 是定义在
是定义在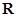 上的偶函数,且
上的偶函数,且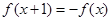 ,若
,若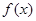 在
在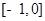 上单调递减,则
上单调递减,则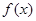 在
在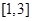 上是( )
上是( )
| A.增函数 | B.减函数 | C.先增后减的函数 | D.先减后增的函数 |
D
解析试题分析:因为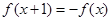 ,所以
,所以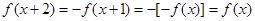 ,所以函数
,所以函数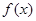 的周期为
的周期为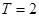 ,因为
,因为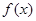 在
在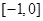 单调递减,所以
单调递减,所以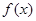 在
在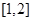 即单调递减,又因为函数
即单调递减,又因为函数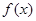 是定义在
是定义在 上的偶函数,由
上的偶函数,由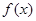 在
在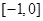 单调递减,可知函数
单调递减,可知函数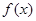 在
在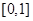 单调递增,从而函数
单调递增,从而函数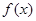 在
在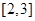 也单调递增,所以函数在
也单调递增,所以函数在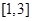 先减后增,故选D.
先减后增,故选D.
考点:1.函数的奇偶性;2.函数的单调性;3.函数的周期性.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
下列函数中,在定义域内是单调递增函数的是( )
A.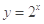 | B.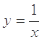 | C.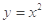 | D. |
已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )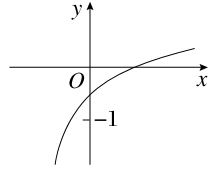
A.0<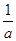 <b<1 <b<1 |
B.0<b<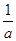 <1 <1 |
C.0<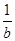 <a<1 <a<1 |
D.0<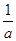 < <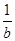 <1 <1 |
已知周期函数f(x)的定义域为R,周期为2,且当-1<x≤1时,f(x)=1-x2.若直线y=-x+a与曲线y=f(x)恰有2个交点,则实数a的所有可能取值构成的集合为( )
A.{a|a=2k+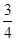 或2k+ 或2k+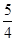 ,k∈Z} ,k∈Z} |
B.{a|a=2k-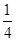 或2k+ 或2k+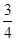 ,k∈Z} ,k∈Z} |
C.{a|a=2k+1或2k+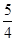 ,k∈Z} ,k∈Z} |
| D.{a|a=2k+1,k∈Z} |
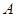 的水平距离10千米处下降,已知下降飞行轨迹为某三次函数图像的一部分,则函数的解析式为( )
的水平距离10千米处下降,已知下降飞行轨迹为某三次函数图像的一部分,则函数的解析式为( )
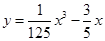
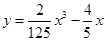
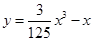
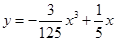
 ,另一种平均价格曲线
,另一种平均价格曲线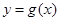 ,如
,如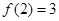 表示股票开始买卖后2小时的即时价格为3元;
表示股票开始买卖后2小时的即时价格为3元;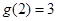 表示2小时内的平均价格为3元.下面给出了四个图像,实线表示
表示2小时内的平均价格为3元.下面给出了四个图像,实线表示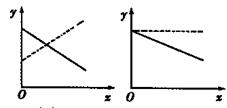
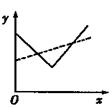
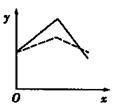
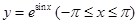 的大致图象为 ( )
的大致图象为 ( )
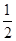 ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0,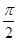 ]上的值域为( )
]上的值域为( )
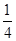 x2+sin(
x2+sin(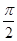 +x),f′(x)为f(x)的导函数,则f′(x)的图象是( )
+x),f′(x)为f(x)的导函数,则f′(x)的图象是( )