题目内容
有下列命题:①命题“?x∈R,使得x2+1>3x”的否定是“?x∈R,都有x2+1≤3x”;
②设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”;
③“a>2”是“a>5”的必要条件;
④若函数f(x)=(x+1)(x+a)为偶函数,则a=-1;
⑤将函数y=sin(2x)(x∈R)的图象向右平移
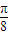 个单位即可得到函数
个单位即可得到函数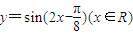 的图象;
的图象;其中所有正确的说法序号是 .
【答案】分析:①命题“?x∈R,使得x2+1>3x”的否定是“?x∈R,都有x2+1≤3x”,由全称命题的否定的书写规则判断其正误;
②设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”,由或命题的否定的书写规则判断其正误;
③“a>2”是“a>5”的必要条件,由必要条件的定义判断;
④若函数f(x)=(x+1)(x+a)为偶函数,则a=-1,由偶函数的性质建立方程求出a的值,进行验证;
⑤将函数y=sin(2x)(x∈R)的图象向右平移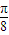 个单位即可得到函数
个单位即可得到函数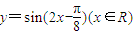 的图象由三角函数图象的变换规则判断其正误.
的图象由三角函数图象的变换规则判断其正误.
解答:解:①命题“?x∈R,使得x2+1>3x”的否定是“?x∈R,都有x2+1≤3x”是一个真命题,因为命题“?x∈R,使得x2+1>3x”是一个特称命题,其否定“?x∈R,都有x2+1≤3x”是一个全称命题,符合命题的否定的书写规则;
②设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”是一个真命题,因为或命题的否定是一个且命题;
③“a>2”是“a>5”的必要条件是一个真命题,因为“a>2”成立不一定得出“a>5”,而“a>5”可以得出“a>2”故命题正确;
④若函数f(x)=(x+1)(x+a)为偶函数,则a=-1,是一个真命题,因为函数解析式可变为f(x)=x2+(a+1)x+a,由函数是偶函数,可得到a=1;
⑤将函数y=sin(2x)(x∈R)的图象向右平移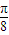 个单位即可得到函数
个单位即可得到函数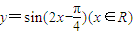 的图象,故原命题错误
的图象,故原命题错误
综上①②③④是正确命题
故答案为①②③④
点评:本题考查必要条件的判断,特称命题的否定,或命题的否定及三角函数的图象的变换,本题涉及到的知识点较多,解题的关键是全面掌握这些知识,知识型题,全面掌握掌握知识是解题的基础,本题的难点是全称命题的否定的书写,
②设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”,由或命题的否定的书写规则判断其正误;
③“a>2”是“a>5”的必要条件,由必要条件的定义判断;
④若函数f(x)=(x+1)(x+a)为偶函数,则a=-1,由偶函数的性质建立方程求出a的值,进行验证;
⑤将函数y=sin(2x)(x∈R)的图象向右平移
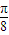 个单位即可得到函数
个单位即可得到函数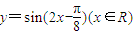 的图象由三角函数图象的变换规则判断其正误.
的图象由三角函数图象的变换规则判断其正误.解答:解:①命题“?x∈R,使得x2+1>3x”的否定是“?x∈R,都有x2+1≤3x”是一个真命题,因为命题“?x∈R,使得x2+1>3x”是一个特称命题,其否定“?x∈R,都有x2+1≤3x”是一个全称命题,符合命题的否定的书写规则;
②设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”是一个真命题,因为或命题的否定是一个且命题;
③“a>2”是“a>5”的必要条件是一个真命题,因为“a>2”成立不一定得出“a>5”,而“a>5”可以得出“a>2”故命题正确;
④若函数f(x)=(x+1)(x+a)为偶函数,则a=-1,是一个真命题,因为函数解析式可变为f(x)=x2+(a+1)x+a,由函数是偶函数,可得到a=1;
⑤将函数y=sin(2x)(x∈R)的图象向右平移
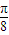 个单位即可得到函数
个单位即可得到函数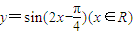 的图象,故原命题错误
的图象,故原命题错误综上①②③④是正确命题
故答案为①②③④
点评:本题考查必要条件的判断,特称命题的否定,或命题的否定及三角函数的图象的变换,本题涉及到的知识点较多,解题的关键是全面掌握这些知识,知识型题,全面掌握掌握知识是解题的基础,本题的难点是全称命题的否定的书写,

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 M”的逆否命题是:若b∈M,则a
M”的逆否命题是:若b∈M,则a x0∈R,x
x0∈R,x -x0-1>0”的否定
-x0-1>0”的否定 P:“
P:“ x∈R,x2-x-1≤0”.
x∈R,x2-x-1≤0”.