题目内容
下列说法:①函数
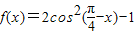 是最小正周期为π的偶函数;
是最小正周期为π的偶函数;②函数
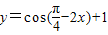 可以改写为
可以改写为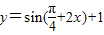 ;
;③函数
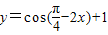 的图象关于直线
的图象关于直线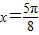 对称;
对称;④函数y=tanx的图象的所有的对称中心为(kπ,0),k∈Z;
⑤将函数y=sin2x的图象先向左平移
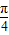 个单位,然后纵坐标不变,横坐标伸长为原来
个单位,然后纵坐标不变,横坐标伸长为原来的2倍,所得图象的函数解析式是
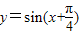 ;
;其中所有正确的命题的序号是 .(请将正确的序号填在横线上)
【答案】分析:①把函数解析式利用二倍角的余弦函数公式及诱导公式化简为一个角的正弦函数,找出ω的值,代入周期公式求出函数的最小正周期,且根据正弦函数为奇函数,得到函数f(x)也为奇函数,即可作出判断;
②根据诱导公式化简函数解析式,即可作出判断;
③由②化简得到的函数解析式,令其角度等于kπ,求出x的解,判断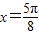 属于求出的x的解集,故本选项正确;
属于求出的x的解集,故本选项正确;
④先根据正切函数是奇函数,因而原点(0,0)是它的对称中心,以及周期性可知点(kπ,0)都是它的对称中心,然后平移坐标系,使原点(0,0)移到(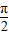 ,0)得到y=tan(x+
,0)得到y=tan(x+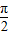 )=-cotx,依旧是奇函数,点(kπ-
)=-cotx,依旧是奇函数,点(kπ-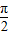 ,0)也是对称中心,综合到一起就得到对称中心是(k
,0)也是对称中心,综合到一起就得到对称中心是(k 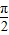 +
+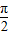 ,0).(k是整数);
,0).(k是整数);
⑤先根据“左加右减”的平移规律把函数解析式进行变形,然后再根据伸缩规律把解析式中x变为 x,即可得到变换后的解析式,作出判断.
x,即可得到变换后的解析式,作出判断.
解答:解:①函数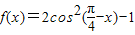
=cos(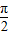 -2x)
-2x)
=sin2x,
∵ω=2,∴T=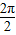 =π,
=π,
又正弦函数为奇函数,∴f(x)为奇函数,
则f(x)为周期为π的奇函数,本选项错误;
②函数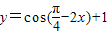
=cos[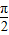 -(
-(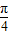 +2x)]+1
+2x)]+1
=sin(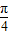 +2x)+1,本选项正确;
+2x)+1,本选项正确;
③函数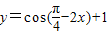
=cos[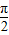 -(
-(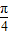 +2x)]
+2x)]
=sin(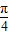 +2x),
+2x),
令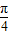 +2x=kπ,(k∈Z)
+2x=kπ,(k∈Z)
解得x=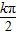 -
-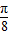 ,
,
∵k=4时,x=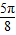 ,
,
则函数图象关于直线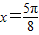 对称,本选项正确;
对称,本选项正确;
④tan(-x)=-tanx,因此正切函数是奇函数,因而原点(0,0)是它的对称中心.
又因为正切函数的周期是π,所以点(kπ,0)都是它的对称中心.
平移坐标系,使原点(0,0)移到(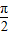 ,0)得到y=tan(x+
,0)得到y=tan(x+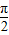 )=-cotx,依旧是奇函数,
)=-cotx,依旧是奇函数,
所以在新坐标系中点(kπ,0)也是对称中心,返回原坐标系,这些点的原坐标是(kπ-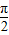 ,0)
,0)
综合到一起就得到对称中心是(k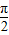 +
+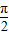 ,0).(k是整数),本选项错误;
,0).(k是整数),本选项错误;
⑤将函数y=sin2x的图象先向左平移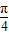 个单位,
个单位,
得到y=sin2(x+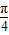 ),
),
然后纵坐标不变,横坐标伸长为原来的2倍,
所得图象的函数解析式为y=sin2( x+
x+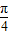 )=sin(x+
)=sin(x+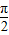 )≠
)≠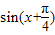 ,
,
本选项错误,
则正确选项的序号为:②③.
故答案为:②③
点评:此题综合考查了三角函数的周期性及其求法,三角函数的恒等变形,余弦函数的对称性,以及三角函数的图象变换规律,涉及的知识有:二倍角的余弦函数公式,诱导公式,函数奇偶性的判断,以及函数平移的规律,要求学生要融汇贯穿,灵活运用所学知识解决问题.
②根据诱导公式化简函数解析式,即可作出判断;
③由②化简得到的函数解析式,令其角度等于kπ,求出x的解,判断
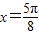 属于求出的x的解集,故本选项正确;
属于求出的x的解集,故本选项正确;④先根据正切函数是奇函数,因而原点(0,0)是它的对称中心,以及周期性可知点(kπ,0)都是它的对称中心,然后平移坐标系,使原点(0,0)移到(
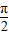 ,0)得到y=tan(x+
,0)得到y=tan(x+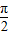 )=-cotx,依旧是奇函数,点(kπ-
)=-cotx,依旧是奇函数,点(kπ-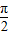 ,0)也是对称中心,综合到一起就得到对称中心是(k
,0)也是对称中心,综合到一起就得到对称中心是(k 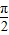 +
+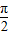 ,0).(k是整数);
,0).(k是整数);⑤先根据“左加右减”的平移规律把函数解析式进行变形,然后再根据伸缩规律把解析式中x变为
 x,即可得到变换后的解析式,作出判断.
x,即可得到变换后的解析式,作出判断.解答:解:①函数
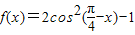
=cos(
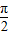 -2x)
-2x)=sin2x,
∵ω=2,∴T=
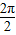 =π,
=π,又正弦函数为奇函数,∴f(x)为奇函数,
则f(x)为周期为π的奇函数,本选项错误;
②函数
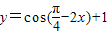
=cos[
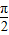 -(
-(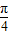 +2x)]+1
+2x)]+1=sin(
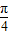 +2x)+1,本选项正确;
+2x)+1,本选项正确;③函数
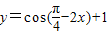
=cos[
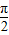 -(
-(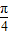 +2x)]
+2x)]=sin(
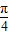 +2x),
+2x),令
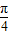 +2x=kπ,(k∈Z)
+2x=kπ,(k∈Z)解得x=
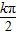 -
-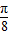 ,
,∵k=4时,x=
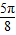 ,
,则函数图象关于直线
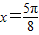 对称,本选项正确;
对称,本选项正确;④tan(-x)=-tanx,因此正切函数是奇函数,因而原点(0,0)是它的对称中心.
又因为正切函数的周期是π,所以点(kπ,0)都是它的对称中心.
平移坐标系,使原点(0,0)移到(
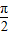 ,0)得到y=tan(x+
,0)得到y=tan(x+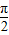 )=-cotx,依旧是奇函数,
)=-cotx,依旧是奇函数,所以在新坐标系中点(kπ,0)也是对称中心,返回原坐标系,这些点的原坐标是(kπ-
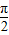 ,0)
,0)综合到一起就得到对称中心是(k
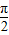 +
+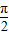 ,0).(k是整数),本选项错误;
,0).(k是整数),本选项错误;⑤将函数y=sin2x的图象先向左平移
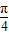 个单位,
个单位,得到y=sin2(x+
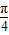 ),
),然后纵坐标不变,横坐标伸长为原来的2倍,
所得图象的函数解析式为y=sin2(
 x+
x+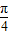 )=sin(x+
)=sin(x+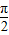 )≠
)≠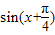 ,
,本选项错误,
则正确选项的序号为:②③.
故答案为:②③
点评:此题综合考查了三角函数的周期性及其求法,三角函数的恒等变形,余弦函数的对称性,以及三角函数的图象变换规律,涉及的知识有:二倍角的余弦函数公式,诱导公式,函数奇偶性的判断,以及函数平移的规律,要求学生要融汇贯穿,灵活运用所学知识解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一个偶函数定义在[-7,7]上,它在[0,7]上的图象如图,下列说法正确的是( )
一个偶函数定义在[-7,7]上,它在[0,7]上的图象如图,下列说法正确的是( )