Question

【题目】设函数f（x）=|1﹣|
（1）求满足f（x）=2的x值；
（2）是否存在实数a，b，且0＜a＜b＜1，使得函数y=f（x）在区间[a，b]上的值域为[a，2b]，若存在，求出a，b的值；若不存在，请说明理由．

Answer 1

【答案】解：（1）由f（x）=2知|1﹣|=2，所以=-1或=3，于是x=﹣1或x=
（2）因为当x∈（0，1）时，
易知f（x）在（0，1）上是减函数，又0＜a＜b＜1，y=f（x）在区间[a，b]上的值域为[a，2b]
所以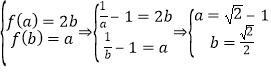
【解析】（1）利用函数的零点，去掉绝对值符号，即可求满足f（x）=2的x值；
（2）化简函数y=f（x）的表达式，判断函数的单调性，然后利用在区间[a，b]上的值域为[a，2b]，列出关于a，b的方程即可求出结果．
【考点精析】本题主要考查了函数的零点的相关知识点，需要掌握函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点才能正确解答此题．