题目内容
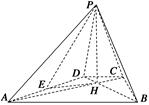
如图,四棱锥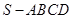 中,
中, 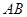 ∥
∥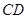 ,
,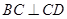 ,侧面
,侧面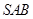 为等边三角形.
为等边三角形.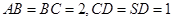 .
.
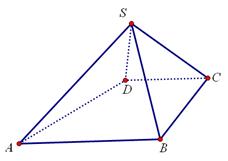
(1)证明: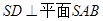
(2)求AB与平面SBC所成角的正弦值。
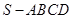 中,
中, 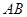 ∥
∥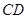 ,
,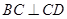 ,侧面
,侧面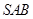 为等边三角形.
为等边三角形.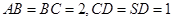 .
.
(1)证明:
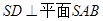
(2)求AB与平面SBC所成角的正弦值。
(1)详见解析(2)见解析
试题分析:(1)SD与两条相交直线AB、SE都垂直,利用线面垂直的判定定理,所以
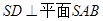 (2)利用面面垂直的性质定理,作
(2)利用面面垂直的性质定理,作 ,垂足为F,
,垂足为F, 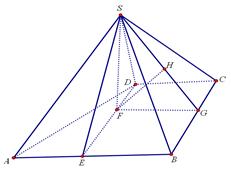
则
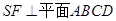 ,作
,作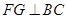 ,垂足为G,所以AB与平面SBC所成的角等于FG与平面SBC所成的角,进一步利用直角三角形边角关系可得AB与平面SBC所成角的正弦值.
,垂足为G,所以AB与平面SBC所成的角等于FG与平面SBC所成的角,进一步利用直角三角形边角关系可得AB与平面SBC所成角的正弦值.(1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2。
连结SE,则

又SD=1,故
 所以
所以 为直角。
为直角。由
 ,得
,得
所以

SD与两条相交直线AB、SE都垂直。 所以
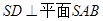
(2)由
 知,
知, 作
作 ,垂足为F,
,垂足为F,
则
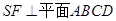 ,
,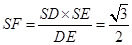
作
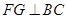 ,垂足为G,则FG=DC=1。且
,垂足为G,则FG=DC=1。且 ,
,所以AB与平面SBC所成的角等于FG与平面SBC所成的角。
连结SG,则

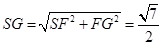
又
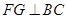 ,
,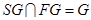 ,
,故
 ,
,作
 ,H为垂足,则
,H为垂足,则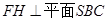 .
.从而FG与平面所成的角为
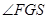
因为
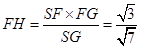 所以
所以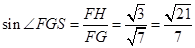

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
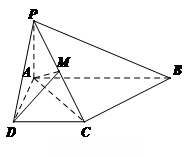
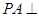 平面ABCD,AD//BC,
平面ABCD,AD//BC,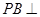 AC,
AC,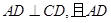
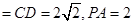 ,点M在线段PD上.
,点M在线段PD上.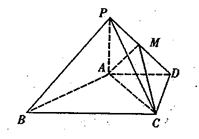
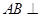 平面PAC;
平面PAC;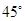 ,试确定点M的位置.
,试确定点M的位置.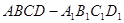 中,
中,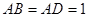 ,
,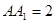 ,点
,点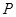 为
为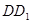 的中点。
的中点。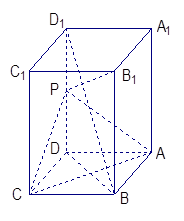
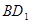 ∥平面
∥平面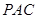 ;
;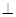 平面
平面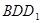 ;
;
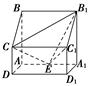
 ,求线段AM的长.
,求线段AM的长.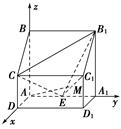
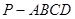 中,
中,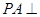 平面
平面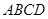 ,底面
,底面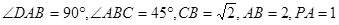 .
.
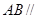 平面
平面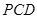 ;
; 平面
平面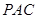 ;
;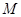 是
是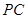 的中点,求三棱锥
的中点,求三棱锥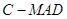 的体积.
的体积.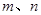 是不同的直线,
是不同的直线,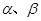 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: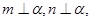 则
则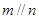
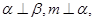 则
则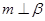
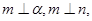 则
则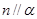
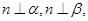 则
则