题目内容
(理)已知函数f(x)=x,g(x)=ln(1+x),h(x)=(1)证明当x>0时,恒有f(x)>g(x);
(2)当x>0时,不等式g(x)>![]() (k≥0)恒成立,求实数k的取值范围;
(k≥0)恒成立,求实数k的取值范围;
(3)在x轴正半轴上有一动点D(x,0),过D作x轴的垂线依次交函数f(x)、g(x)、h(x)的图象于点A、B、C,O为坐标原点.试将△AOB与△BOC的面积比表示为x的函数m(x),并判断m(x)是否存在极值,若存在,求出极值;若不存在,请说明理由.
(文)已知函数f(x)=![]() ,x∈(0,+∞),数列{an}满足a1=1,an+1=f(an);数列{bn}满足b1=1,bn+1=
,x∈(0,+∞),数列{an}满足a1=1,an+1=f(an);数列{bn}满足b1=1,bn+1=![]() ,其中Sn为数列{bn}的前n项和,n=1,2,3,….
,其中Sn为数列{bn}的前n项和,n=1,2,3,….
(1)求数列{an}和数列{bn}的通项公式;
(2)设Tn=![]() ,证明Tn<3.
,证明Tn<3.
答案:(理)(1)证明:设F(x)=f(x)-g(x),则F′(x)=![]() ,
,
当x>0时,F′(x)>0,所以函数F(x)在(0,+∞)上单调递增.又F(x)在x=0处连续,所以F(x)>F(0)=0,即f(x)-g(x)>0.所以f(x)>g(x).
(2)解:设G(x)=g(x)![]() ,则G(x)在(0,+∞)上恒大于0,G(x)=ln(1+x)-k+
,则G(x)在(0,+∞)上恒大于0,G(x)=ln(1+x)-k+![]() ,
,
G′(x)=![]() ,
,
x2+(2k-k2)x=0的根为0和k2-2k,即在区间(0,+∞)上,G′(x)=0的根为0和k2-2k,若k2-2k>0,则G(x)在(0,k2-2k)上单调递减,且G(0)=0,与G(x)在(0,+∞)上恒大于0矛盾;若k2-2k≤0,G(x)在(0,+∞)上单调递增,且G(0)=0,满足题设条件,所以k2-2k≤0.所以0≤k≤2.
(3)解:m(x)= ,
,
m′(x)=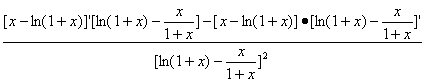 ,
,
其分母为正数,其分子为ln(1+x)·![]() .
.
由第(2)问,知ln(1+x)>![]() 在(0,+∞)上恒成立,所以m′(x)>0在(0,+∞)上恒成立,即m(x)在(0,+∞)上为单调递增函数,故m(x)无极值.
在(0,+∞)上恒成立,所以m′(x)>0在(0,+∞)上恒成立,即m(x)在(0,+∞)上为单调递增函数,故m(x)无极值.
(文)(1)解:∵f(x)=![]() ,an+1=f(an),∴an+1=
,an+1=f(an),∴an+1=![]() .∴
.∴![]() .
.
∴![]() 为以
为以![]() =1为首项、以2为公差的等差数列.∴
=1为首项、以2为公差的等差数列.∴![]() =1+(n-1)·2.∴an=
=1+(n-1)·2.∴an=![]() .
.
又∵f(x)=![]() ,bn+1=
,bn+1=![]() ,∴bn+1=
,∴bn+1=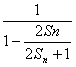 =2Sn+1.
=2Sn+1.
∴bn+2=2Sn+1+1.∴bn+2-bn+1=2(Sn+1-Sn).∴bn+2=3bn+1.∵b1=1,b2=2S1+1=3,∴{bn}为以b1=1为首项、以q=3为公比的等比数列.bn=3n-1.
(2)证明:依题意Tn=1·1+3·![]() +5·(
+5·(![]() )2+7·(
)2+7·(![]() )3+…+(2n-1)(
)3+…+(2n-1)(![]() )n-1,
)n-1,
![]() Tn=1·
Tn=1·![]() +3·(
+3·(![]() )2+5·(
)2+5·(![]() )3+…+(2n-3)·(
)3+…+(2n-3)·(![]() )n-1+(2n-1)·(
)n-1+(2n-1)·(![]() )n,
)n,
∴![]() Tn=1+2[
Tn=1+2[![]() +(
+(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n-1]-(2n-1)·(
)n-1]-(2n-1)·(![]() )n=1+2·
)n=1+2·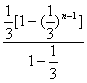 -(2n-1)(
-(2n-1)(![]() )n.
)n.
∴![]() Tn=2-(
Tn=2-(![]() )n-1-(2n-1)(
)n-1-(2n-1)(![]() )n.
)n.
∴Tn=3-![]() ·(
·(![]() )n-1-
)n-1-![]() ·(2n-1)(
·(2n-1)(![]() )n<3.
)n<3.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案
 (理)已知函数
(理)已知函数 (2011•普陀区三模)(理)已知函数
(2011•普陀区三模)(理)已知函数