题目内容
设 为定义在R上的奇函数,且当
为定义在R上的奇函数,且当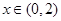 时,
时, ,则
,则
 为定义在R上的奇函数,且当
为定义在R上的奇函数,且当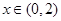 时,
时, ,则
,则
| A.-2 | B.2 | C.-98 | D.98 |
A
分析:由已知当x∈(0,2)时,f(x)=2x,可求出f(1);再由f(x)为定义在R上的奇函数,可知f(-1)=f(1),进而求出答案.
解答:解:∵当x∈(0,2)时,f(x)=2x,∴f(1)=21=2,
又∵f(x)为定义在R上的奇函数,∴f(-x)=-f(x),
∴f(-1)=-f(1)=-2.
故选A.
解答:解:∵当x∈(0,2)时,f(x)=2x,∴f(1)=21=2,
又∵f(x)为定义在R上的奇函数,∴f(-x)=-f(x),
∴f(-1)=-f(1)=-2.
故选A.

练习册系列答案
相关题目
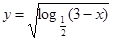 的定义域;
的定义域;
 ,求函数
,求函数 的值域。
的值域。

 的定义域为( )
的定义域为( )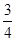 ,1)
,1)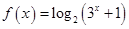 的值域为( )
的值域为( )



 函数
函数 的值域为_________.
的值域为_________. 的定义域是 。
的定义域是 。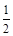 )x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是 )
) 的定义域是
的定义域是