Question

8、若方程lg|x|=-|x|+5在区间（k，k+1）（k∈Z）上有解，则所有满足条件的k的值的和为

-1

．

Answer 1

分析：构造函数y=lg|x|，y=-|x|+5，画出图象，结合函数的奇偶性，推出结论．

解答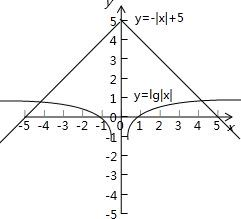：解：由方程可令，y=lg|x|，y=-|x|+5，画出图象，
两个函数都是偶函数，
所以函数图象的交点，关于y轴对称，
因而方程lg|x|=-|x|+5在区间（k，k+1）（k∈Z）上有解，
一根位于（-k-1，-k），另一根位于（k，k+1），
则所有满足条件的k的值的和：-1，
故答案为：-1

点评：本题考查知识点是根的存在性及根的个数判断、函数的应用，函数与方程的思想，数形结合思想，是中档题．