题目内容
已知有公共焦点的椭圆与双曲线中心在原点,焦点在x轴上,左、右焦点分别为F1,F2,且它们在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若PF1=10,双曲线的离心率的取值范围为(1,2),则该椭圆的离心率的取值范围是
(
,
)
| 1 |
| 3 |
| 2 |
| 5 |
(
,
)
.| 1 |
| 3 |
| 2 |
| 5 |
分析:设椭圆的长半轴为a1,双曲线的半实轴长为a2,它们公共的焦距为2c,|PF2|=n,根据椭圆与双曲线的定义建立方程组解出a1=5+c且a2=5-c,得到双曲线的离心率为
∈(1,2),由此解出c的范围再代入椭圆离心率的表达式,利用不等式的性质加以计算,可得该椭圆的离心率的取值范围.
| c |
| 5-c |
解答:解:如图,设椭圆的长半轴为a1,双曲线的半实轴长为a2,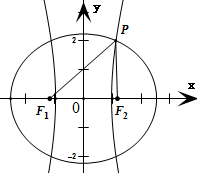
它们公共的焦距为2c,|PF2|=n,
∵|PF1|=10,△PF1F2是以PF1为底边的等腰三角形.
∴由椭圆与双曲线的定义,得
,解之得
,
∵双曲线的离心率的取值范围为(1,2),∴1<
<2,
设
=x,可得c=
,
从而得到椭圆的离心率e=
=
=
-
.
由1<x<2,可得
-
<
-
<
-
,即
<
-
<
.
即该椭圆的离心率的取值范围是(
,
).
故答案为:(
,
)

它们公共的焦距为2c,|PF2|=n,
∵|PF1|=10,△PF1F2是以PF1为底边的等腰三角形.
∴由椭圆与双曲线的定义,得
|
|
∵双曲线的离心率的取值范围为(1,2),∴1<
| c |
| 5-c |
设
| c |
| 5-c |
| 5x |
| 1+x |
从而得到椭圆的离心率e=
| c |
| 5+c |
| x |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 4x+2 |
由1<x<2,可得
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4x+2 |
| 1 |
| 2 |
| 1 |
| 10 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4x+2 |
| 2 |
| 5 |
即该椭圆的离心率的取值范围是(
| 1 |
| 3 |
| 2 |
| 5 |
故答案为:(
| 1 |
| 3 |
| 2 |
| 5 |
点评:本题给出有公共焦点的椭圆与双曲线,在双曲线离心率的取值范围为(1,2)时求椭圆的离心率的取值范围.着重考查了椭圆、双曲线的定义与标准方程,利用不等式的基本性质求变量取值范围等知识,属于中档题.

练习册系列答案
相关题目
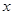 轴上,左右焦点分别为
轴上,左右焦点分别为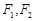 ,且它们在第一象限的交点为P,
,且它们在第一象限的交点为P,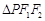 是以
是以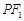 为底边的等腰三角形.若
为底边的等腰三角形.若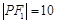 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为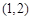 .则该椭圆的离心率的取值范围是
.则该椭圆的离心率的取值范围是