题目内容
对任意![]() ,给定区间
,给定区间![]() ,设函数
,设函数![]() 表示实数
表示实数![]() 与
与![]() 的给定区间内整数之差的绝对值.
的给定区间内整数之差的绝对值.
|
(2)判断函数![]()
![]() R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论;
(3)求方程![]() 的实根.(要求说明理由)
的实根.(要求说明理由)
(1)![]()
(2)证明见解析。
(3)若![]() 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.
解析:
(Ⅰ)当![]() 时,由定义知:
时,由定义知:![]() 与0距离最近,
与0距离最近,![]()
![]()
当![]() 时,由定义知:
时,由定义知:![]() 最近的一个整数,故
最近的一个整数,故
![]()
(Ⅱ)对任何![]() R,函数
R,函数![]() 都存在,且存在
都存在,且存在![]() Z,
Z,
满足![]() Z)
Z)
即![]() Z).
Z).
由(Ⅰ)的结论,![]()
即![]() 是偶函数.
是偶函数.
(Ⅲ)(理科)解:![]()
(1)当![]() 没有大于1的实根;
没有大于1的实根;
(2)容易验证![]() 为方程
为方程![]() 的实根;
的实根;
(3)当![]()
设![]()
则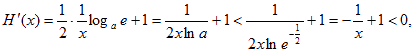
所以当![]() 为减函数,
为减函数,![]()
所以方程没有![]() 的实根;
的实根;
(4)当![]()
设![]() 为减函数,
为减函数,![]() ,
,
所以方程没有![]() 的实根.
的实根.
综上可知,若![]() 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
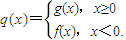 是否存在k,对任意给定的非零实数x1,存在惟一的非零实数x2(x2≠x1),使得q′(x2)=q′(x1)?若存在,求k的值;若不存在,请说明理由.
是否存在k,对任意给定的非零实数x1,存在惟一的非零实数x2(x2≠x1),使得q′(x2)=q′(x1)?若存在,求k的值;若不存在,请说明理由.