题目内容
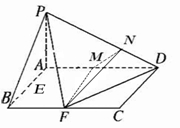
 (2013•自贡一模)如图,四棱锥P-ABCD的底ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,E,F分别是AB,BC的中点N在轴上.
(2013•自贡一模)如图,四棱锥P-ABCD的底ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,E,F分别是AB,BC的中点N在轴上.(I)求证:PF⊥FD;
(II)在PA上找一点G,使得EG∥平面PFD;
(III)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
分析:(I)连接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,利用线面垂直性质定理可得DF⊥PA,再由线面垂直的判定定理得到DF⊥平面PAF,进而可得PF⊥FD;
(Ⅱ)过点E作EH∥FD交AD于点H,过点H作HG∥DP交PA于点G,由此可确定G点位置,使得EG∥平面PFD;
(Ⅲ)确定∠PBA是PB与平面ABCD所成的角,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,确定∠MNF即为二面角A-PD-F的平面角,进而可得结论.
(Ⅱ)过点E作EH∥FD交AD于点H,过点H作HG∥DP交PA于点G,由此可确定G点位置,使得EG∥平面PFD;
(Ⅲ)确定∠PBA是PB与平面ABCD所成的角,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,确定∠MNF即为二面角A-PD-F的平面角,进而可得结论.
解答:(Ⅰ)证明:连接AF,则AF=DF=
又AD=2,∴DF2+AF2=AD2,∴DF⊥AF
又PA⊥平面ABCD,
∴DF⊥PA,又PA∩AF=A,
∴DF⊥平面PAF,PF?平面PAF
∴DF⊥PF;
(Ⅱ)解:过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有AH=
AD
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
AP,
∴平面GEH∥平面PFD,∴EG∥平面PFD.
从而满足AG=
AP的点G即为所求;
(Ⅲ)解:∵PA⊥平面ABCD,
∴∠PBA是PB与平面ABCD所成的角,且∠PBA=45°.
∴PA=AB=1
取AD的中点M,则FM⊥AD,FM⊥平面PAD,
在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,所以∠MNF即为二面角A-PD-F的平面角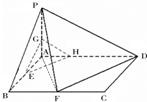
∵Rt△MND∽Rt△PAD,
∴
=
,
∵PA=1,MD=1,PD=
,且∠FMN=90°
∴MN=
,FN=
,cos∠MNF=
=
.
| 2 |

又AD=2,∴DF2+AF2=AD2,∴DF⊥AF
又PA⊥平面ABCD,
∴DF⊥PA,又PA∩AF=A,
∴DF⊥平面PAF,PF?平面PAF
∴DF⊥PF;
(Ⅱ)解:过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有AH=
| 1 |
| 4 |
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
| 1 |
| 4 |
∴平面GEH∥平面PFD,∴EG∥平面PFD.
从而满足AG=
| 1 |
| 4 |
(Ⅲ)解:∵PA⊥平面ABCD,
∴∠PBA是PB与平面ABCD所成的角,且∠PBA=45°.
∴PA=AB=1
取AD的中点M,则FM⊥AD,FM⊥平面PAD,
在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,所以∠MNF即为二面角A-PD-F的平面角

∵Rt△MND∽Rt△PAD,
∴
| MN |
| PA |
| MD |
| PD |
∵PA=1,MD=1,PD=
| 5 |
∴MN=
| ||
| 5 |
| ||
| 5 |
| MN |
| FN |
| ||
| 6 |
点评:本题考查线面垂直的判定,考查线面平行,考查面面角,解题关键是熟练掌握空间线面关系的判定,性质,正确作出面面角.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 (2013•自贡一模)运行如图所示的程序框图,则输出s的值为( )
(2013•自贡一模)运行如图所示的程序框图,则输出s的值为( )