题目内容
已知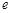 是自然对数底数,若函数
是自然对数底数,若函数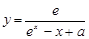 的定义域为
的定义域为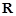 ,则实数
,则实数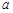 的取值范围为
的取值范围为
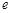 是自然对数底数,若函数
是自然对数底数,若函数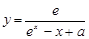 的定义域为
的定义域为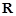 ,则实数
,则实数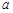 的取值范围为
的取值范围为A. | B. | C.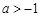 | D.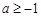 |
C
试题分析:∵函数
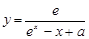 的定义域为
的定义域为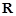 ,∴
,∴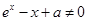 ,当
,当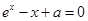 即
即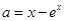 时,令
时,令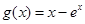 ,则
,则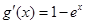 ,令
,令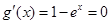 得x=0,令
得x=0,令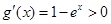 得x<0,令
得x<0,令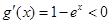 得x>0,可知
得x>0,可知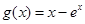 在
在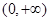 单调递减,在
单调递减,在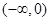 单调递增,故当x=0时,g(x)有最大值
单调递增,故当x=0时,g(x)有最大值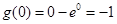 ,所以
,所以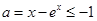 ,根据补集思想可知,当
,根据补集思想可知,当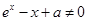 时,实数
时,实数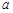 的取值范围为
的取值范围为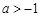 ,故选C
,故选C点评:利用导数法求函数值域是求解此类问题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
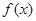 的导函数为
的导函数为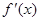 ,函数
,函数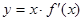 的图象的一部分如图所示,则正确的是
的图象的一部分如图所示,则正确的是 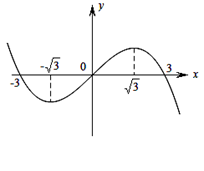
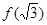 ,极小值为
,极小值为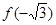
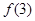 ,极小值为
,极小值为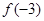
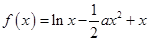 ,
,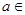 R.
R.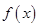 的单调区间;
的单调区间;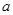 ,使得函数
,使得函数 ?若存在,求
?若存在,求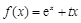 (e为自然对数的底数).
(e为自然对数的底数).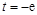 时,求函数
时,求函数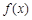 的单调区间;
的单调区间;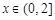 ,不等式
,不等式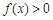 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.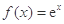 (
( 为自然对数的底数),
为自然对数的底数), (
( ).
).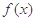
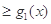 ;
;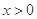 时,比较
时,比较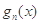 的大小,并说明理由;
的大小,并说明理由;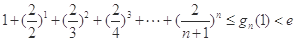 (
(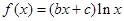 在
在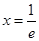 处取得极值,且在
处取得极值,且在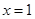 处的切线的斜率为1。
处的切线的斜率为1。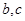 的值及
的值及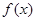 的单调减区间;
的单调减区间;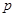 >0,
>0,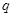 >0,
>0, ,求证:
,求证: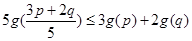 。
。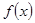 在
在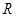 上满足
上满足 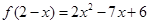 ,则曲线
,则曲线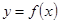 在
在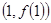 处的切线方程是
处的切线方程是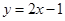
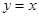
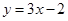
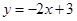
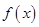 的导数为
的导数为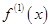 ,
,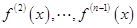 的导数为
的导数为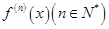 。若
。若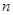 次求导,则
次求导,则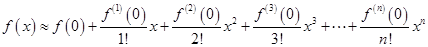
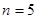 ,根据这个结论,则可近似估计自然对数的底数
,根据这个结论,则可近似估计自然对数的底数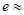 _____(用分数表示).
_____(用分数表示).