题目内容
已知两条直线m,n,两个平面α,β.下面四个命题中不正确的是( )
分析:A.利用结论“两条平行线中的一条垂直于平面,则另一条也垂直于这个平面”即可判断;
B.同上;
C.可能有n?α,因此不全面;
D.如图所示,可利用线面、面面垂直的判定和性质定理证明正确.
B.同上;
C.可能有n?α,因此不全面;
D.如图所示,可利用线面、面面垂直的判定和性质定理证明正确.
解答:解:A.根据“两条平行线中的一条垂直于平面,则另一条也垂直于这个平面”,得m∥n,m⊥α⇒n⊥α,正确;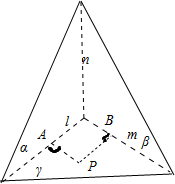
B.根据同上,正确;
C.由m∥n,m∥α,可得n∥α或n?α,故不正确;
D.如图所示:设α∩γ=l,β∩γ=m,取点P∈γ,过点P作PA⊥l,PB⊥m,垂足分别为A、B,
∵α⊥γ,β⊥γ,∴PA⊥α,PB⊥β,
又∵α∩β=n,∴PA⊥n,PB⊥n,∴n⊥γ,故正确.
综上可知:不正确的是C.
故选C.

B.根据同上,正确;
C.由m∥n,m∥α,可得n∥α或n?α,故不正确;
D.如图所示:设α∩γ=l,β∩γ=m,取点P∈γ,过点P作PA⊥l,PB⊥m,垂足分别为A、B,
∵α⊥γ,β⊥γ,∴PA⊥α,PB⊥β,
又∵α∩β=n,∴PA⊥n,PB⊥n,∴n⊥γ,故正确.
综上可知:不正确的是C.
故选C.
点评:熟练正确线线、线面、面面的平行与垂直的性质与判定定理是解题的关键.

练习册系列答案
相关题目