题目内容
设a,b为正实数.现有下列命题:
①若a2-b2=1,则a-b<1;
②若
-
=1,则a-b<1;
③若|
-
|=1,则|a-b|<1;
④若|a3-b3|=1,则|a-b|<1.
其中的真命题有 .(写出所有真命题的编号)
【答案】
①④
【解析】①中,若a,b都小于1,则a-b<1;
若a,b中至少有一个大于等于1,则a+b>1,
由a2-b2=(a+b)(a-b)=1,
所以a-b<1,故①正确.
②中
-
=
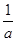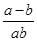=1,只需a-b=ab即可,
取a=2,b=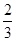
满足上式但a-b=
>1,故②错;
③中,|a-b|=|(
-
)(+)|=|+|>|-|=1,故③错;
④中,对于|a3-b3|=|(a-b)(a2+ab+b2)|=1,
若a,b中至少有一个大于等于1,
则a2+ab+b2>1,则|a-b|<1,
若a,b都小于1,则|a-b|<1,所以④正确.
综上,真命题有①④.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为
已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O、O′，现将此三棱柱绕直线OO′旋转（包括逆时针方向和顺时针方向），射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积记为S（x），则函数S（x）的最大值和最小正周期分别是（ ）
已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O、O′，现将此三棱柱绕直线OO′旋转（包括逆时针方向和顺时针方向），射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积记为S（x），则函数S（x）的最大值和最小正周期分别是
，
