Question

（2012•泸州一模）如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=

1

2

AD=1，CD=

3

，二面角M-BO-C的大小为30°．
（Ⅰ）求证：平面POB⊥平面PAD；
（Ⅱ）求直线BM与CD所成角的余弦值．

Answer 1

分析：（Ⅰ）根据AD∥BC，BC=

1

2

AD，O为AD的中点可得四边形BCDO为平行四边形，则CD∥BO，从而OB⊥AD，平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD，根据面面垂直的性质可知，BO⊥平面PAD，而BQ?平面POB，满足面面垂直的判定定理，从而证得结论．
（Ⅱ）以O为原点建立空间直角坐标系．则平面BOC的法向量为

n

=(0，0，1)；O，P，B，设M（x，y，z），求出M点坐标，利用cos∠OBM=|

BM • BO

| BM || BO |

|，求出直线BM与CD所成角的余弦值．

解答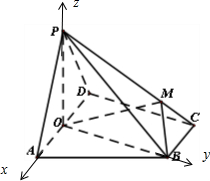：解答：解：（Ⅰ）证明：∵AD∥BC，BC=

1

2

AD，O为AD的中点，
∴四边形BCDO为平行四边形，
∴CD∥BO．         
∵∠ADC=90°
∴∠AOB=90°  即OB⊥AD．
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD，
∴BO⊥平面PAD．             
∵BO?平面POB，
∴平面POB⊥平面PAD．      
（Ⅱ）∵PA=PD，O为AD的中点，∴PO⊥AD．
∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PO⊥平面ABCD．
（不证明PO⊥平面ABCD直接建系扣1分）
如图，以O为原点建立空间直角坐标系．
则平面BOC的法向量为

n

=(0，0，1)；O（0，0，0），P(0，0，

3

)，B(0，

3

，0)，
C(-1，

3

，0)．
设M（x，y，z），
则

PM

=(x，y，z-

3

)，

MC

=(-1-x，

3

-y，-z)，
∵

PM

=t

MC

，
∴

x=t(-1-x) y=t( 3 -y) z- 3 =t(-z)

，
∴

x=- t 1+t y= 3 t 1+t z= 3 1+t

，
在平面MBO中，

OB

 =(0，

3

，0)，

OM

=(-

t

1+t

，

3 t

1+t

，

3

1+t

)，
∴平面MBO法向量为

m

=(

3

，0，t)．
∵二面角M-BO-C为30°，cos30°=

n • m

| n || m |

=

t

3+0+t2

=

3

2

，
∴t=3． 

CP

=(1，-

3

，

3

)，

OM

=

OC

+

1

4

CP

=(-1，

3

，0)+

1

4

(1，-

3

，

3

)=(-

3

4

，

3 3

4

，

3

4

)，

BM

=

BO

+

OM

=(-

3

4

，-

3

4

，

3

4

)
cos∠OBM=|

BM • BO

| BM || BO |

|=|

- 3 4

15 4 3

|=

5

5

．

点评：点评：本题考查平面与平面垂直，直线与直线所成的角的求法，几何体的体积的求法，考查空间想象能力，计算能力．