题目内容
已知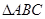 中,
中,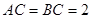 ,
,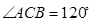 ,
,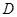 为
为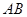 的中点,
的中点,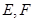 分别在线段
分别在线段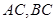 上的动点,且
上的动点,且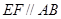 ,
,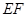 交
交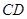 于
于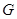 ,把
,把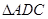 沿
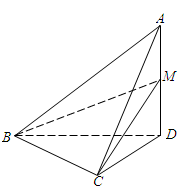
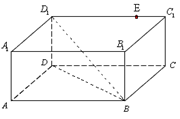
沿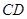 折起,如下图所示,
折起,如下图所示,
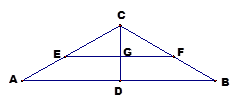
(Ⅰ)求证: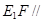 平面
平面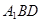 ;
;
(Ⅱ)当二面角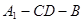 为直二面角时,是否存在点
为直二面角时,是否存在点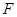 ,使得直线
,使得直线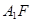 与平面
与平面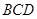 所成的角为
所成的角为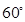 ,若存在求
,若存在求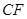 的长,若不存在说明理由。
的长,若不存在说明理由。
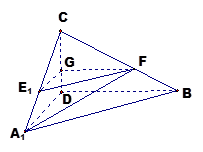
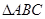 中,
中,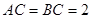 ,
,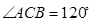 ,
,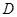 为
为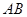 的中点,
的中点,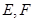 分别在线段
分别在线段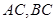 上的动点,且
上的动点,且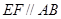 ,
,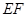 交
交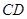 于
于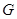 ,把
,把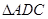 沿
沿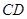 折起,如下图所示,
折起,如下图所示,
(Ⅰ)求证:
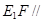 平面
平面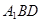 ;
;(Ⅱ)当二面角
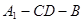 为直二面角时,是否存在点
为直二面角时,是否存在点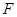 ,使得直线
,使得直线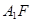 与平面
与平面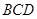 所成的角为
所成的角为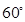 ,若存在求
,若存在求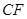 的长,若不存在说明理由。
的长,若不存在说明理由。
(Ⅰ)详见解析;(Ⅱ)存在,且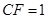 .
.
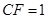 .
.试题分析:(Ⅰ)这是一个折叠问题,做这一类题,需比较折叠前的图形与折叠后的图形,找那些量发生变化,那些量没发生变化,本题求证:
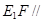 平面
平面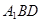 ,证明线面平行,可先证线线平行,也可先证面面平行,注意到,
,证明线面平行,可先证线线平行,也可先证面面平行,注意到,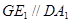 ,
,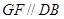 ,可证面面平行,即证平面
,可证面面平行,即证平面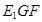 //平面
//平面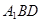 即可;(Ⅱ)当二面角
即可;(Ⅱ)当二面角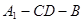 为直二面角时,是否存在点
为直二面角时,是否存在点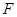 ,使得直线
,使得直线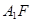 与平面
与平面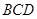 所成的角为
所成的角为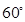 ,此属探索性命题,解此类题一般都先假设存在,若求出线段长,就存在,否则就不存在,此题因为二面角
,此属探索性命题,解此类题一般都先假设存在,若求出线段长,就存在,否则就不存在,此题因为二面角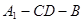 为直二面角,则
为直二面角,则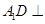 平面
平面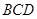 ,故
,故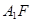 与平面
与平面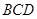 所成角为
所成角为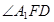 ,求出
,求出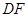 的长,从而得
的长,从而得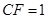 ,故存在点
,故存在点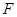 ,且
,且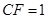 .
.试题解析:(Ⅰ)
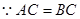 ,又
,又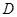 为
为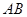 的中点
的中点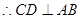 ,又
,又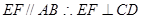 2分
2分在空间几何体
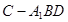 中,
中,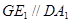 ,则
,则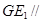 平面
平面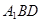 ,
,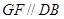 ,则
,则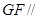 平面
平面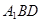 ,
, 平面
平面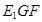 //平面
//平面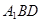 ,
,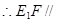 平面
平面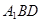 6分
6分(Ⅱ)∵二面角
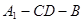 为直二面角,
为直二面角, 平面
平面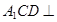 平面
平面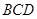
 ,
,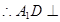 平面
平面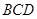 , 8分
, 8分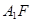 在平面
在平面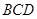 内的射影为
内的射影为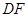 ,
,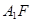 与平面
与平面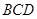 所成角为
所成角为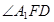 ,
,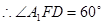 10分
10分由于

 ,
,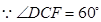 ,
,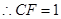 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
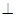 平面ADC;
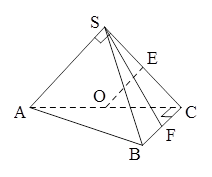
平面ADC; 中,侧面
中,侧面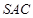 与底面
与底面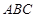 垂直,
垂直, 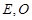 分别是
分别是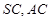 的中点,
的中点,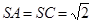 ,
,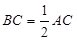 ,
,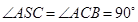 .
.
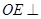 平面
平面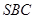 ;
;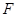 为线段
为线段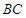 的中点,求异面直线
的中点,求异面直线 与
与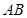 所成角的正切值.
所成角的正切值. 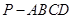 中,底面
中,底面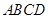 为菱形,
为菱形,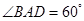 ,
,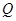 为
为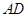 的中点.
的中点.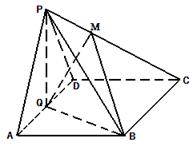
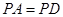 ,求证:平面
,求证:平面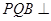 平面
平面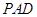 ;
;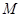 在线段
在线段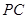 上,
上,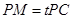 ,试确定
,试确定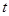 的值,使
的值,使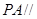 平面
平面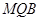 .
.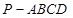 的底面是正方形,
的底面是正方形,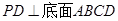 ,点
,点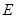 在棱
在棱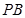 上.
上.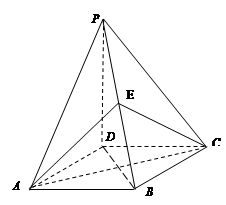
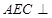 平面
平面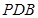 ;
;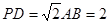 ,且
,且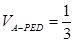 时,确定点
时,确定点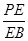 的值.
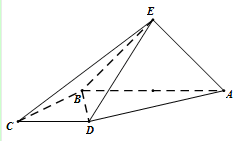
的值.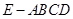 中,面
中,面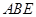
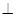 面
面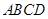 ,底面
,底面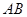 ∥
∥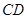 ,
,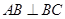 ,
,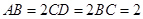 ,
,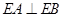 .
.
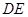 的位置关系;
的位置关系;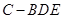 的体积;
的体积;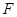 是线段
是线段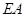 上一点,当
上一点,当 //平面
//平面 时,求
时,求 的长.
的长.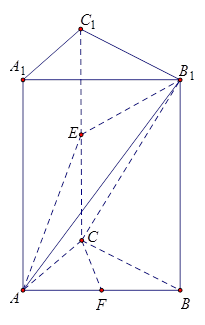
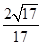 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.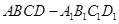 中,底面
中,底面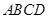 为正方形,
为正方形,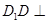 面
面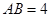 ,
,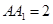 ,点
,点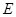 在棱
在棱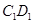 上,且
上,且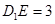 .
.
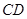 上确定一点
上确定一点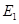 ,使得直线
,使得直线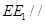 平面
平面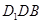 ,并证明;
,并证明;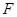 在底面
在底面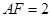 ,请说明点
,请说明点 长度的最小值.
长度的最小值.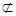 α,则n∥α;
α,则n∥α;