题目内容
已知平面内动点P到两定点F1,F2的距离的和等于常数2a,关于动点P的轨迹正确的说法是 .
①点P的轨迹一定是椭圆;
②2a>|F1F2|时,点P的轨迹是椭圆;
③2a=|F1F2|时,点P的轨迹是线段F1F2;
④点P的轨迹一定存在;
⑤点P的轨迹不一定存在.
①点P的轨迹一定是椭圆;
②2a>|F1F2|时,点P的轨迹是椭圆;
③2a=|F1F2|时,点P的轨迹是线段F1F2;
④点P的轨迹一定存在;
⑤点P的轨迹不一定存在.
分析:由平面内动点P到两定点F1,F2的距离的和等于常数2a,可得:当2a>|F1F2|时,点P的轨迹是椭圆;
当2a=|F1F2|时,点P的轨迹是线段F1F2; 当2a<|F1F2|时,动点P的轨迹不存在.即可判断出答案.
当2a=|F1F2|时,点P的轨迹是线段F1F2; 当2a<|F1F2|时,动点P的轨迹不存在.即可判断出答案.
解答:解:由平面内动点P到两定点F1,F2的距离的和等于常数2a,可知:
当2a>|F1F2|时,点P的轨迹是椭圆;当2a=|F1F2|时,点P的轨迹是线段F1F2; 当2a<|F1F2|时,动点P的轨迹不存在.
由以上结论可知:只有②③⑤正确.
故答案为:②③⑤.
当2a>|F1F2|时,点P的轨迹是椭圆;当2a=|F1F2|时,点P的轨迹是线段F1F2; 当2a<|F1F2|时,动点P的轨迹不存在.
由以上结论可知:只有②③⑤正确.
故答案为:②③⑤.
点评:本题考查了椭圆的定义、分类讨论的思想方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
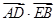 的最小值.
的最小值.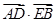 的最小值.
的最小值.