题目内容
方程ay=b2x2+c中的a,b,c∈{-2,0,1,2,3},且a,b,c互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有
- A.28条
- B.32条
- C.36条
- D.48条
B
分析:方程变形得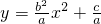 ,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况,利用列举法可解.
,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况,利用列举法可解.
解答:方程变形得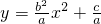 ,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况:
,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况:
(1)若b=-2时,a=1,c=0,2,3或a=2,c=0,1,3或a=3,c=0,1,2;
(2)若b=2时,a=-2,c=0,1,3或a=1,c=0,2,3或a=3,c=0,1,-2;
以上两种情况下有4条重复,故共有9+5=14条;
同理 若b=1,共有9条; 若b=3时,共有9条.
综上,共有14+9+9=32种
故选B.
点评:此题难度很大,若采用排列组合公式计算,很容易忽视重复的9条抛物线.列举法是解决排列、组合、概率等非常有效的办法,要能熟练运用.
分析:方程变形得
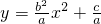 ,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况,利用列举法可解.
,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况,利用列举法可解.解答:方程变形得
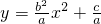 ,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况:
,若表示抛物线,则a≠0,b≠0,所以分b=-2,1,2,3四种情况:(1)若b=-2时,a=1,c=0,2,3或a=2,c=0,1,3或a=3,c=0,1,2;
(2)若b=2时,a=-2,c=0,1,3或a=1,c=0,2,3或a=3,c=0,1,-2;
以上两种情况下有4条重复,故共有9+5=14条;
同理 若b=1,共有9条; 若b=3时,共有9条.
综上,共有14+9+9=32种
故选B.
点评:此题难度很大,若采用排列组合公式计算,很容易忽视重复的9条抛物线.列举法是解决排列、组合、概率等非常有效的办法,要能熟练运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目