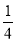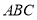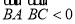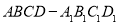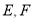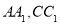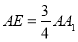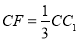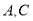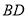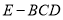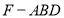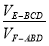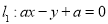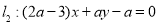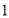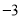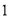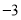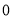题目内容
如图,已知圆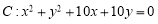 ,点
,点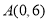 .
.
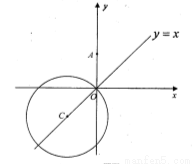
(1)求圆心在直线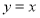 上,经过点
上,经过点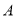 ,且与圆
,且与圆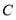 相外切的圆
相外切的圆 的方程;
的方程;
(2)若过点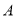 的直线
的直线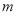 与圆
与圆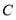 交于
交于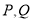 两点,且圆弧
两点,且圆弧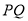 恰为圆
恰为圆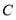 周长的
周长的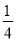 ,求直线
,求直线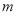 的方程.
的方程.
(1) ;(2)
;(2)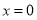 或
或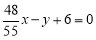 .
.
【解析】
试题分析:由圆心在直线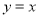 上,设出圆心
上,设出圆心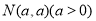 ,根据圆
,根据圆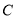 与圆
与圆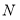 相切,得到点为切点,表示半径,由
相切,得到点为切点,表示半径,由 ,求
,求 的值,即可求出圆
的值,即可求出圆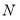 的方程;(2)先考虑直线斜率不存在的情况,
的方程;(2)先考虑直线斜率不存在的情况, 显然满足题意;后考虑直线
显然满足题意;后考虑直线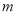 斜率存在的情况,由对称性得到圆心到直线
斜率存在的情况,由对称性得到圆心到直线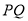 的距离为5,设出直线
的距离为5,设出直线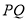 的方程,利用点到直线的距离公式求出
的方程,利用点到直线的距离公式求出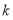 的值,确定此时直线
的值,确定此时直线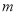 的方程,综上,得到所有满足题意直线
的方程,综上,得到所有满足题意直线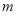 的方程.
的方程.
试题解析:(1)由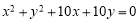 ,得
,得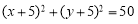 2分
2分
所以圆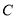 的圆心坐标为
的圆心坐标为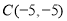
又圆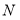 的圆心在直线
的圆心在直线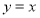 上
上
依题意可知两圆外切于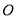 点,设圆
点,设圆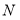 的圆心坐标为
的圆心坐标为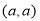 3分
3分
则有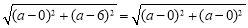 ,解得
,解得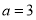 4分
4分
所以圆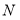 的圆心坐标为
的圆心坐标为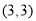 ,半径
,半径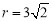 5分
5分
故圆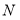 的方程为
的方程为
综上可知,圆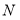 的方程为
的方程为 6分
6分
(Ⅱ)因为圆弧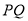 恰为圆
恰为圆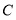 圆周的
圆周的 , 所以
, 所以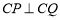 8分
8分
所以点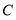 到直线
到直线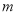 的距离为5 9分
的距离为5 9分
当直线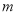 的斜率不存在时,点
的斜率不存在时,点 到
到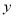 轴的距离为5,直线
轴的距离为5,直线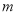 即为
即为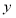 轴
轴
所以此时直线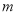 的方程为
的方程为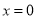 11分
11分
当直线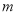 的斜率存在时,设直线
的斜率存在时,设直线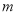 的方程为
的方程为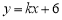 ,即
,即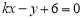
所以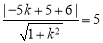 12分
12分
解得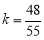 13分
13分
所以此时直线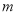 的方程为
的方程为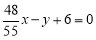
故所求直线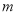 的方程为
的方程为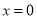 或
或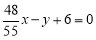 . 14分
. 14分
考点:1.直线与圆的位置关系;2.圆的方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目