题目内容
等轴双曲线C:x2-y2=a2与抛物线y2=16x的准线交于A,B两点,|AB|=4,则双曲线C的实轴长等于
4
| 3 |
4
.| 3 |
分析:根据双曲线方程,求出抛物线的准线方程,利用|AB|=4,即可求得结论.
解答:解:∵抛物线y2=16x,2p=16,p=8,∴
=4.
∴抛物线的准线方程为x=-4.
设等轴双曲线与抛物线的准线x=-4的两个交点A(-4,y),B(-4,-y)(y>0),
则|AB|=|y-(-y)|=2y=4,∴y=2.
将x=-4,y=2 代入双曲线C:x2-y2=a2,得(-4)2-2 2=a2,
∴a2=12,a=2
,即2a=4
,
∴双曲线C的实轴长等于:4
.
故答案为:4
.
| p |
| 2 |
∴抛物线的准线方程为x=-4.
设等轴双曲线与抛物线的准线x=-4的两个交点A(-4,y),B(-4,-y)(y>0),
则|AB|=|y-(-y)|=2y=4,∴y=2.
将x=-4,y=2 代入双曲线C:x2-y2=a2,得(-4)2-2 2=a2,
∴a2=12,a=2
| 3 |
| 3 |
∴双曲线C的实轴长等于:4
| 3 |
故答案为:4
| 3 |
点评:本题考查抛物线,双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
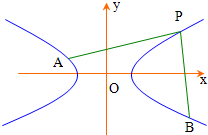 (2005•武汉模拟)已知等轴双曲线C:x2-y2=a2 (a>0)上一定点P(x0,y0)及曲线C上两动点AB满足(
(2005•武汉模拟)已知等轴双曲线C:x2-y2=a2 (a>0)上一定点P(x0,y0)及曲线C上两动点AB满足(