题目内容
在极坐标系中,动点P(ρ,θ)运动时,ρ与 成反比,动点P的轨迹经过点(2,0).
成反比,动点P的轨迹经过点(2,0).
(1)求动点P的轨迹的极坐标方程;
(2)将(1)中极坐标方程化为直角坐标方程,并指出轨迹是何种曲线.
(1) ;(2)y=-
;(2)y=- x2+1
x2+1
解析试题分析:(1)利用ρ与 成反比例以及点P轨迹过定点(2,0)求解.(2)记住极坐标与直角坐标之间转化的公式
成反比例以及点P轨迹过定点(2,0)求解.(2)记住极坐标与直角坐标之间转化的公式 ,分别代入即可求解.
,分别代入即可求解.
设 ∵2=
∵2= ,∴k=1. ∴
,∴k=1. ∴
(2)∵ρ+ρsin θ=2,∴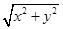 +y=2.整理得y=-
+y=2.整理得y=- x2+1.∴轨迹为开口向下,顶点为(0,1)的抛物线.
x2+1.∴轨迹为开口向下,顶点为(0,1)的抛物线.
考点:极坐标方程.

练习册系列答案
相关题目
 ,圆M的参数方程为
,圆M的参数方程为 。求:(1)将直线的极坐标方程化为直角坐标方程;
。求:(1)将直线的极坐标方程化为直角坐标方程; 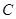 的极坐标方程为
的极坐标方程为 ,现以极点
,现以极点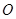 为原点,极轴为
为原点,极轴为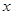 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线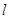 的参数方程为
的参数方程为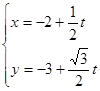 (
(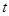 为参数)
为参数) (a>b>0,
(a>b>0, 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M 对应的参数
对应的参数 ,
,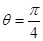 与曲线C2交于点D
与曲线C2交于点D
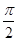 )是曲线C1上的两点,求
)是曲线C1上的两点,求 的值。
的值。 ,直线的极坐标方程为ρcos
,直线的极坐标方程为ρcos =a,且点A在直线上.
=a,且点A在直线上. ,(α为参数),试判断直线与圆的位置关系.
,(α为参数),试判断直线与圆的位置关系. )=
)=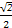 .
. 化为对应的直角坐标方程是 。
化为对应的直角坐标方程是 。 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.