题目内容
已知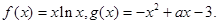
(1)求函数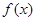 的最小值;
的最小值;
(2)对一切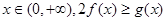 恒成立,求实数
恒成立,求实数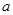 的取值范围;
的取值范围;
(3)证明:对一切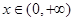 ,都有
,都有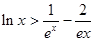 成立.
成立.
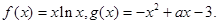
(1)求函数
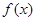 的最小值;
的最小值;(2)对一切
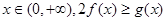 恒成立,求实数
恒成立,求实数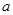 的取值范围;
的取值范围;(3)证明:对一切
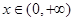 ,都有
,都有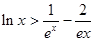 成立.
成立.(1)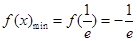 ;(2)
;(2)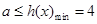 (3)见解析
(3)见解析
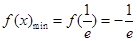 ;(2)
;(2)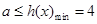 (3)见解析
(3)见解析试题分析:(1)先求定义域,再利用导数与单调性的关系求单调区间;(2)通过导数解决不等式恒成立的问题;(3)先转化不等式,在给定的区间内比较大小.
(1)由已知知函数
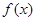 的定义域为
的定义域为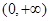 ,
,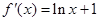 , 1分
, 1分当
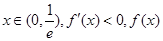 单调递减, 2分
单调递减, 2分当
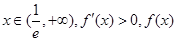 单调递增. 3分
单调递增. 3分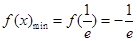 . 4分
. 4分(2)
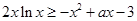 ,则
,则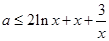 , 5分
, 5分设
 ,则
,则 , 6分
, 6分 ①
 单调递减;
单调递减;②
 单调递增;
单调递增;
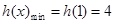 ,对一切
,对一切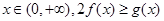 恒成立,
恒成立,
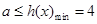 . 8分
. 8分(3)原不等式等价于
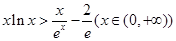 , 9分
, 9分由(1)可知
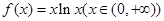 的最小值是
的最小值是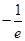 ,当且仅当
,当且仅当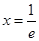 时取到最小值. 10分
时取到最小值. 10分设
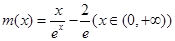 ,则
,则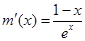 ,
,易知
 ,当且仅当
,当且仅当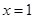 时取到最小值.&科&
时取到最小值.&科&从而对一切
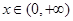 ,都有
,都有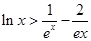 成立. 12分
成立. 12分
练习册系列答案
相关题目

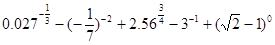
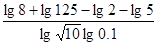
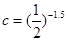 ,则( ).
,则( ).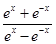 的图象大致为( )
的图象大致为( )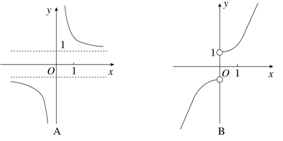
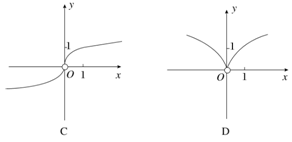
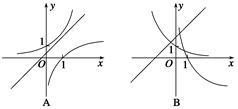

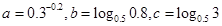 ,那么
,那么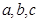 的大小关系是( )
的大小关系是( )



 ,
, ,
, ,则( )
,则( )

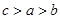
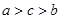
 则
则 ________.
________.