题目内容
(1)设 ,是两个非零向量,如果
,是两个非零向量,如果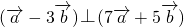 ,且
,且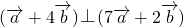 ,求向量
,求向量 与
与 的夹角大小;
的夹角大小;
(2)用向量方法证明:设平面上A,B,C,D四点满足条件AD⊥BC,BD⊥AC,则AB⊥CD.
解:(1)因为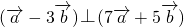 ,所以
,所以 ,
,
因为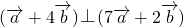 ,所以
,所以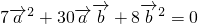 ,(2分)
,(2分)
两式相减得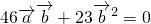 ,于是
,于是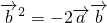 ,
,
将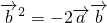 代回任一式得
代回任一式得 ,(6分)
,(6分)
设与的夹角为θ,则 =
= ,
,
所以与的夹角大小为120°.(8分)
(2)因AD⊥BC,所以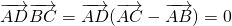 ,
,
因BD⊥AC,所以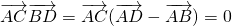 ,(12分)
,(12分)
于是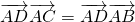 ,
,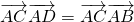 ,
,
所以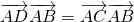 ,
,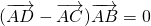 ,(14分)
,(14分)
即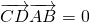 ,所以
,所以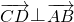 ,即AB⊥CD.(16分)
,即AB⊥CD.(16分)
分析:(1))由已知可得, ,
,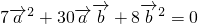 ,整理可得
,整理可得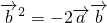 ,
,
将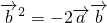 代回原式可得
代回原式可得 ,根据向量的夹角公式可求
,根据向量的夹角公式可求
(2)由AD⊥BC,可得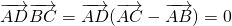 ,同理可得
,同理可得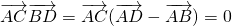
要证AB⊥CD即证即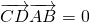
点评:本题主要考查了平面向量的数量积的性质:若 ?
? 的应用,要证明线段垂直只要证明对应的向量的数量积为0即可,而若知道向量垂直,则可得向量的数量积为0
的应用,要证明线段垂直只要证明对应的向量的数量积为0即可,而若知道向量垂直,则可得向量的数量积为0
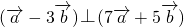 ,所以
,所以 ,
,因为
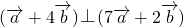 ,所以
,所以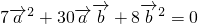 ,(2分)
,(2分)两式相减得
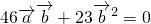 ,于是
,于是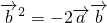 ,
,将
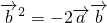 代回任一式得
代回任一式得 ,(6分)
,(6分)设与的夹角为θ,则
 =
= ,
,所以与的夹角大小为120°.(8分)
(2)因AD⊥BC,所以
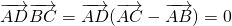 ,
,因BD⊥AC,所以
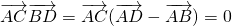 ,(12分)
,(12分)于是
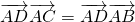 ,
,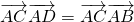 ,
,所以
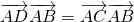 ,
,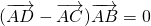 ,(14分)
,(14分)即
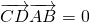 ,所以
,所以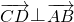 ,即AB⊥CD.(16分)
,即AB⊥CD.(16分)分析:(1))由已知可得,
 ,
,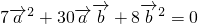 ,整理可得
,整理可得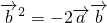 ,
,将
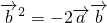 代回原式可得
代回原式可得 ,根据向量的夹角公式可求
,根据向量的夹角公式可求(2)由AD⊥BC,可得
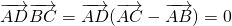 ,同理可得
,同理可得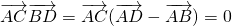
要证AB⊥CD即证即
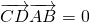
点评:本题主要考查了平面向量的数量积的性质:若
 ?
? 的应用,要证明线段垂直只要证明对应的向量的数量积为0即可,而若知道向量垂直,则可得向量的数量积为0
的应用,要证明线段垂直只要证明对应的向量的数量积为0即可,而若知道向量垂直,则可得向量的数量积为0 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
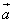 ,
,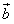 是两个非零向量,如果
是两个非零向量,如果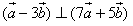 ,且
,且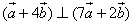 ,求向量
,求向量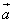 与
与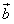 的夹角大小;
的夹角大小;