题目内容
设a、b是两个非零实数，给出下列三个不等式：①a5+b5＞a3b2+a2b3；②a2+b2≥2（a-b-1）；③
| a |
| b |
| b |
| a |
其中恒成立的不等式是
分析：令a=b，我们可以判断①的真假；根据实数的性质，我们可得（a-1）2+（b+1）2≥0，进而判断②的真假；根据基本不等式，我们可以求出
+
的取值范围，进而得到答案．
| a |
| b |
| b |
| a |
解答：解：若a=b，则a5+b5=a3b2+a2b3，故①不恒成立；
∵（a-1）2+（b+1）2≥0恒成立，故②a2+b2≥2（a-b-1）恒成立；
当a，b异号时，
+
≤-2，当a，b同号时，
+
≥2，故③不恒成立；
故答案为：②
∵（a-1）2+（b+1）2≥0恒成立，故②a2+b2≥2（a-b-1）恒成立；
当a，b异号时，
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
故答案为：②
点评：本题考查的知识点是不等式，其中熟练掌握基本不等式及相应的推论是解答本题的关键．
练习册系列答案
相关题目
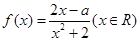在区间
上是增函数，实数
组成集合
；设关于
的方程
的两个非零实根
实数
使得不等式
使得对任意
及
恒成立，则
B.
D.
(其中a,b为实常数)。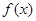
的单调区间：
时，函数
：
上是减函数，设关于x的方程
的两个非零实数根为
，
。试问是否存在实数m,使得
对任意满足条件的a及t
恒成立？若存在，求m的取值范围；若不存在，请说明理由。