题目内容
已知椭圆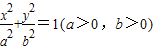 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为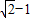 .
.(I)求椭圆方程;
(II)已知经过点F的动直线l与椭圆交于不同的两点A、B,点M(
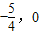 ),证明:
),证明: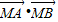 为定值.
为定值.
【答案】分析:(I)先求出圆心坐标,再根据题意求出a、b,得椭圆的标准方程.
(II)根据直线的斜率是否存在,分情况设直线方程,再与椭圆方程联立方程组,设出交点坐标,结合韦达定理根与系数的关系,利用向量坐标运算验证.
解答:解:(I)∵圆x2+y2+2x=0的圆心为(-1,0),依据题意c=1,a-c=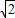 -1,∴a=
-1,∴a=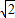 .
.
∴椭圆的标准方程是: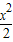 +y2=1;
+y2=1;
(II)①当直线L与x轴垂直时,L的方程是:x=-1,
得A(-1,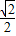 ),B(-1,-
),B(-1,-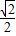 ),
),
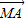 •
•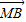 =(
=( ,
,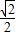 )•(
)•( ,-
,-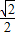 )=-
)=-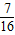 .
.
②当直线L与x轴不垂直时,设直线L的方程为 y=k(x+1)
 ⇒(1+2k2)x2+4k2x+2k2-2=0,
⇒(1+2k2)x2+4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),则x1x2=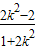 ,x1+x2=-
,x1+x2=-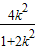 ,
,
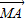
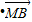 =(x1+
=(x1+ ,y1)•(x2+
,y1)•(x2+ ,y2)=x1x2+
,y2)=x1x2+ (x1+x2)+
(x1+x2)+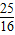 +k2(x1x2+x1+x2+1)
+k2(x1x2+x1+x2+1)
=(1+k2)x1x2+(k2+ )(x1+x2)+k2+
)(x1+x2)+k2+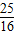 =(1+k2)(
=(1+k2)( )+(k2+
)+(k2+ )(-
)(-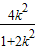 )+k2+
)+k2+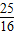
=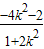 +
+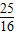 =-2+
=-2+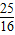 =-
=-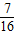
综上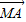 •
•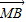 为定值-
为定值-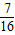 .
.
点评:本题考查直线与圆锥曲线的综合问题及向量坐标运算.根据韦达定理,巧妙利用根与系数的关系设而不求,是解决本类问题的关键.
(II)根据直线的斜率是否存在,分情况设直线方程,再与椭圆方程联立方程组,设出交点坐标,结合韦达定理根与系数的关系,利用向量坐标运算验证.
解答:解:(I)∵圆x2+y2+2x=0的圆心为(-1,0),依据题意c=1,a-c=
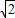 -1,∴a=
-1,∴a=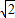 .
.∴椭圆的标准方程是:
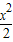 +y2=1;
+y2=1;(II)①当直线L与x轴垂直时,L的方程是:x=-1,
得A(-1,
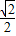 ),B(-1,-
),B(-1,-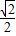 ),
),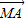 •
•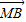 =(
=( ,
,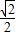 )•(
)•( ,-
,-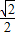 )=-
)=-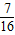 .
.②当直线L与x轴不垂直时,设直线L的方程为 y=k(x+1)
 ⇒(1+2k2)x2+4k2x+2k2-2=0,
⇒(1+2k2)x2+4k2x+2k2-2=0,设A(x1,y1),B(x2,y2),则x1x2=
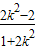 ,x1+x2=-
,x1+x2=-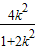 ,
,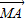
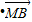 =(x1+
=(x1+ ,y1)•(x2+
,y1)•(x2+ ,y2)=x1x2+
,y2)=x1x2+ (x1+x2)+
(x1+x2)+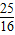 +k2(x1x2+x1+x2+1)
+k2(x1x2+x1+x2+1)=(1+k2)x1x2+(k2+
 )(x1+x2)+k2+
)(x1+x2)+k2+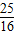 =(1+k2)(
=(1+k2)( )+(k2+
)+(k2+ )(-
)(-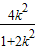 )+k2+
)+k2+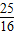
=
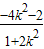 +
+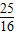 =-2+
=-2+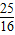 =-
=-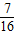
综上
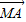 •
•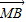 为定值-
为定值-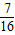 .
.点评:本题考查直线与圆锥曲线的综合问题及向量坐标运算.根据韦达定理,巧妙利用根与系数的关系设而不求,是解决本类问题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
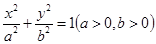 的左焦点F为圆
的左焦点F为圆 的圆心,且椭圆上的点到点F的距离最小值为
的圆心,且椭圆上的点到点F的距离最小值为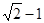 。
。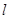 与椭圆交于不同的两点A、B,点M(
与椭圆交于不同的两点A、B,点M(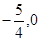 ),证明:
),证明: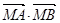 为定值。
为定值。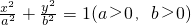 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为 .
.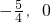 ),证明:
),证明: 为定值.
为定值.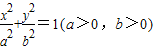 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为 .
. ),证明:
),证明: 为定值.
为定值.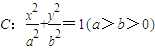 的左焦点F及点A(0,b),原点O到直线FA的距离为
的左焦点F及点A(0,b),原点O到直线FA的距离为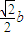 .
.