Question

在△ABC所在平面a外有一点P，且PA=PB=PC，则P在a内的射影是△ABC的（　　）

Answer 1

分析：令点P在平面ABC上的投影为O，利用已知条件，结合勾股定理，证明出OA=OB=OC，进而根据三角形五心的定义，得到结论．

解答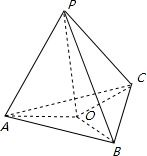：解：设点P作平面ABC的射影O，由题意：PA=PB=PC，因为PO⊥底面ABC，
所以△PAO≌△POB≌△POC
即：OA=OB=OC
所以O为三角形的外心．
故选D．

点评：本题考查棱锥的结构特征，三角形五心的定义，考查逻辑思维能力，是基础题．