题目内容
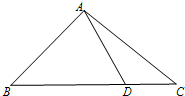
在△ABC中,∠B=45°,AC=| 10 |
| 3 |
| 5 |
(1)求AB边的长度;
(2)若点D是AB的中点,求中线CD的长度.
分析:(1)利用二倍角公式及同角三角函数的基本关系求出sinC的值,再由正弦定理求得AB的值.
(2)三角形中由余弦定理求出BC的值,再利用余弦定理求出CD的值.
(2)三角形中由余弦定理求出BC的值,再利用余弦定理求出CD的值.
解答:解:(1)∵cos2C=
,∴1-2sin2C=
(1分),解得:sinC=
(负值舍去).(3分)
由正弦定理:
=
,即
=
(4分),可得AB=
•
×
=2(6分).
(2)∵AC2=AB2+BC2-2AB•BCcosB,(7分) 即10=4+BC2-4BCcos45°,解得BC=3
. (10分)
由于 CD2=BD2+BC2-2BD•BCcosB=1+18-2×1×3
×
=13,(13分)
故CD=
.(14分)
| 3 |
| 5 |
| 3 |
| 5 |
| ||
| 5 |
由正弦定理:
| AB |
| sinC |
| AC |
| sinB |
| AB | ||||
|
| ||||
|
| 10 |
| 2 |
| ||
| 5 |
(2)∵AC2=AB2+BC2-2AB•BCcosB,(7分) 即10=4+BC2-4BCcos45°,解得BC=3
| 2 |
由于 CD2=BD2+BC2-2BD•BCcosB=1+18-2×1×3
| 2 |
| ||
| 2 |
故CD=
| 13 |
点评:本题考查利用正弦定理、余弦定理解三角形,同角三角函数的基本关系,利用正弦定理、余弦定理,是解题的关键.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
在△ABC中,∠B=90°,AC=
,D,E两点分别在AB,AC上.使
=
=2,DE=3.将△ABC沿DE折成直二面角,则二面角A-EC-B的余弦值为( )
| 15 |
| 2 |
| AD |
| DB |
| AE |
| EC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,∠B=
,三边长a,b,c成等差数列,且a,
,c成等比数列,则b的值是( )
| π |
| 3 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|