题目内容
某中学在高一开设了数学史等4门不同的选修课，每个学生必须选修，且只能从中选一门．该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同．
(1)求3个学生选择了3门不同的选修课的概率；
(2)求恰有2门选修课这3个学生都没有选择的概率；
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数，求X的分布列．
(1)求3个学生选择了3门不同的选修课的概率；
(2)求恰有2门选修课这3个学生都没有选择的概率；
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数，求X的分布列．
（1）
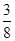（2）
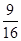（3）X的概率分布表为：
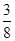（2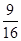）（3）X的概率分布表为：| X | 0 | 1 | 2 | 3 |
| P |  | |  |  |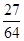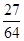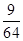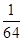
(1)3个学生选择了3门不同的选修课的概率：P1＝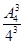
＝.
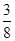(2)恰有2门选修课这3个学生都没有选择的概率：P2＝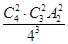
＝.
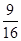(3)X＝0，1，2，3，则有P(ξ＝0)＝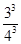
＝；
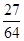P(X＝1)＝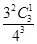
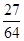＝；P(X＝2)＝
＝；
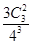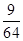P(X＝3)＝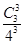
＝.
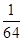∴X的概率分布表为：
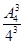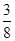＝.(2)恰有2门选修课这3个学生都没有选择的概率：P2＝
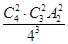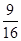＝.(3)X＝0，1，2，3，则有P(ξ＝0)＝
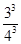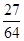＝；P(X＝1)＝
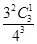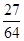＝；P(X＝2)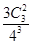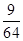＝＝；P(X＝3)＝
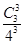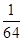＝.∴X的概率分布表为：
| X | 0 | 1 | 2 | 3 |
| P | | | | |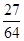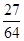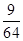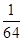
练习册系列答案
相关题目
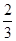，乙的命中率为P2，在射击比赛活动中每人射击两发子弹则完成一次检测，在一次检测中，若两人命中数相等且都不少于一发，则称该射击小组为“先进和谐组”．
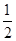，求该小组在一次检测中荣获“先进和谐组”的概率；
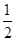，参加第五项不合格的概率为
.
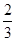.且
.
，求随机变量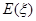
.