题目内容
5.已知x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$求:(1)z=x2+y2-10y+25的最小值和最大值;
(2)z=$\frac{y+1}{x+1}$的取值范围.
分析 (1)作出可行域,z=x2+y2-10y+25=x2+(y-5)2表示区域内的点到D(0,5)的距离平方,数形结合可得;
(2)z=$\frac{y+1}{x+1}$表示区域内的点与E(-1,-1)连线的斜率,数形结合可得.
解答  解:(1)作出$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$所对应的可行域(如图阴影△ABC),
解:(1)作出$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$所对应的可行域(如图阴影△ABC),
z=x2+y2-10y+25=x2+(y-5)2表示区域内的点到D(0,5)的距离平方,
数形结合可得D到直线x-y+2=0的距离d=$\frac{|0-5+2|}{\sqrt{{1}^{2}+(-1)^{2}}}$=$\frac{3}{\sqrt{2}}$,
∴z的最小值为($\frac{3}{\sqrt{2}}$)2=$\frac{9}{2}$,
联立$\left\{\begin{array}{l}{x-y+2=0}\\{2x-y-5=0}\end{array}\right.$可解得C(7,9),
由两点间的距离公式可得DC=$\sqrt{{7}^{2}+(9-5)^{2}}$=$\sqrt{65}$,
∴z的最大值为($\sqrt{65}$)2=65;
(2)z=$\frac{y+1}{x+1}$表示区域内的点与E(-1,-1)连线的斜率,
数形结合可得当直线经过点B(3,1)时z取最小值$\frac{1}{2}$,
当直线经过点A(1,3)时z取最大值2.
∴z=$\frac{y+1}{x+1}$的取值范围为[$\frac{1}{2}$,1]
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
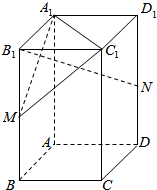 正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.
正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.