题目内容
如图,在半径为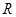 、圆心角为
、圆心角为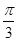 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形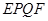 ,并且
,并且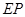 与
与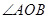 的平分线
的平分线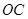 平行,设
平行,设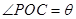 .
.
(1)试写出用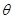 表示长方形
表示长方形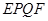 的面积
的面积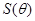 的函数;
的函数;
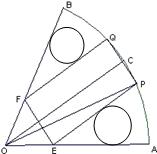
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形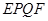 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
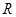 、圆心角为
、圆心角为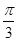 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形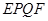 ,并且
,并且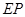 与
与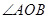 的平分线
的平分线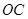 平行,设
平行,设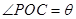 .
.
(1)试写出用
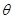 表示长方形
表示长方形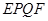 的面积
的面积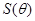 的函数;
的函数;(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形
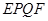 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.(1) (2)
(2) .
.
 (2)
(2) .
. 试题分析:(1)由条件得
 ,
,从而
 4分
4分(2)由(1)得
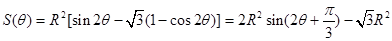 ,
,所以当
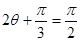 时,即
时,即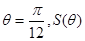 取得最大值,为
取得最大值,为 7分
7分此时
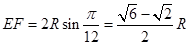 ,
, ,
,所以
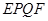 为正方形,依题意知制成的圆柱底面应是由
为正方形,依题意知制成的圆柱底面应是由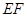 围成的圆,
围成的圆,从而由周长
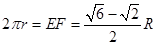 ,得其半径为
,得其半径为 . 11分
. 11分
另一方面,如图所示,设圆与
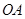 边切于点
边切于点 ,连结
,连结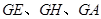 ,
, .
.设两小圆的半径为
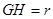 ,则
,则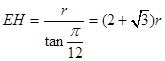 ,
,且
 ,从而
,从而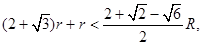 所以
所以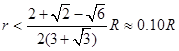 ,
,因
 ,
,所以能作出满足条件的两个圆.此时圆柱的体积
 .……………16分
.……………16分点评:中档题,结合图形特征,利用直角三角形中的边角关系,建立函数模型。确定函数最值过程中,可利用导数。

练习册系列答案
相关题目
 =( )
=( )



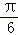
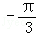
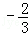 π
π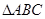 中用余弦定理解得
中用余弦定理解得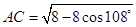 ,乙同学在
,乙同学在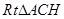 中解得
中解得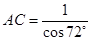 ,据此可得
,据此可得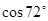 的值所在区间为( )
的值所在区间为( )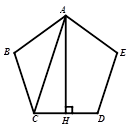




 的终边上一点
的终边上一点 ,则锐角
,则锐角


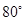
 的值等于
的值等于



 的终边经过点
的终边经过点 ,则
,则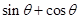 的值为( )
的值为( )




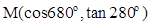 位于直角坐标面的
位于直角坐标面的